Bevor wir Computern mithilfe von Schaltwerken das Rechnen im Dualsystem beibringen, schauen wir uns selbst an, wie man in diesem System rechnet. Wir werden uns dabei auf die Addition und die Subtraktion beschränken.
Zum Aufwärmen erinnern wir uns daran, wie die schriftliche Addition im Dezimalsystem funktioniert.
Wiedergabe stellt eine Verbindung zu YouTube her.
Die schriftliche Addition von Dualzahlen funktioniert ganz genauso! Der einzige Unterschied ist, dass man schon einen Übertrag erhält, wenn man 1 + 1 rechnet, denn im Dualsystem gilt
1(2) + 1(2) = 10(2).
Betrachten wir ein Beispiel. Die kleinen Einsen stellen dabei jeweils den Übertrag dar:
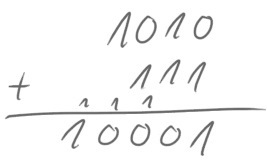
Wiedergabe stellt eine Verbindung zu YouTube her.
Es gibt einen wichtigen Unterschied zwischen Zahlen in der Mathematik und in der Informatik: Ein Computer hat für die Darstellung von Dualzahlen nur eine begrenzte Zahl von Stellen zur Verfügung. Daher ist es oft so, dass Computer von Anfang an eine feste Stellenzahl für Zahlen verwenden.
Nehmen wir einmal an, wir haben einen Computer, der für die Darstellung von Dualzahlen immer vier Stellen benutzt, d.h., für jede Zahl werden vier Bit reserviert. Dann können wir in dem Computer mit den Dualzahlen von 0000(2) bis 1111(2) arbeiten. Dieser Computer kann also nur mit Zahlen zwischen 0(10) und 15(10) rechnen! Das ist natürlich nicht besonders leistungsstark. Aber um das Prinzip zu verstehen, wie die Rechnungen im Computer ablaufen, ist dieser gut für uns geeignet.
Man stellt sich in der Informatik gerne vor, dass die Zahlen in einem Kreis angeordnet sind:
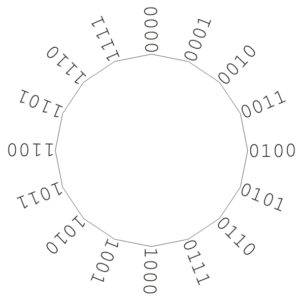
Zählen wir mit unserem Computer weiter als bis 1111(2), so fangen wir deshalb wieder bei 0000(2) an. Wer sehr(!) lange dasselbe Auto fährt, kann das auch beim Kilometerzähler beobachten.
Man kann sich Additionen an diesem Kreis gut veranschaulichen. Nehmen wir zum Beispiel 1011(2)+0011(2). Wir starten dazu bei der 1011(2), gehen 0011(2) = 3(10) Zahlen weiter im Uhrzeigersinn und landen so beim Ergebnis 1110(2).
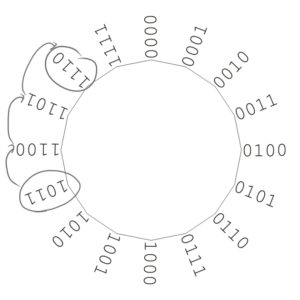
D.h. um Additionen zu veranschaulichen muss man in diesem Kreis im Uhrzeigersinn wandern.
Allerdings klappt das nicht immer. Starten wir zum Beispiel bei der 1011(2) und addieren 0111(2) = 7(10), dann gehen wir sieben Zahlen weiter im Uhrzeigersinn. Dieses Mal überschreiten wir die 0000(2) und landen schließlich bei der 0010(2). Hier hat die Addition nicht funktioniert, denn das richtige Ergebnis lautet eigentlich 10010(2). Weil unser Computer aber nur vier Stellen zur Verfügung hat, kann er das Ergebnis nicht darstellen – es ist einfach zu groß.
Wiedergabe stellt eine Verbindung zu YouTube her.