Binomische Formeln

Inhalt dieser Seite

Es gibt verschiedene Wege, die binomischen Formeln herzuleiten. in den Clips sehen wir eine geometrische / zeichnerische Herleitung und auch noch eine rechnerische.

Erste binomische Formel

Hier wollen wir noch einmal die rechnerische Herleitung kurz wiedergeben. Diese besteht eigentlich nur darin, dass man zwei Klammern ausmultipliziert:

    \begin{align*} (a+b)^2 &= (a+b) \cdot (a+b) & |&\mbox{ausmultiplizieren} \\ &= a\cdot a + a \cdot b + b \cdot a + b \cdot b &| &a\cdot b = b \cdot a\\ &= a^2 + a \cdot b + a \cdot b + b^2 &|&\mbox{zusammenfassen}\\ &= a^2 + 2 \cdot a \cdot b + b^2 \ \end{align*}

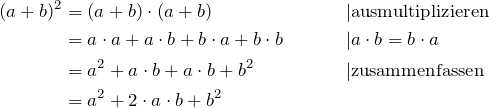
Sehen wir uns ein paar Beispiele an:

    \begin{align*} (a+3)^2 &= a^2 + 2\cdot a \cdot 3 + 3^2\\ &= a^2 + 6\cdot a + 9\\ &\\ (5+b)^2 &= 5^2 + 2\cdot 5 \cdot b + b^2\\ &= 25 + 10 \cdot b + b^2\\ \end{align*}


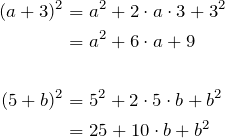
Wiedergabe stellt eine Verbindung zu YouTube her.

Zweite binomische Formel


Wiedergabe stellt eine Verbindung zu YouTube her.

Die dritte sieht ein wenig anders aus:

    \[(a+b) \cdot (a-b) = a^2 - b^2\]

Keywords: Binomische Formel, quadratische Gleichung