Bedingte Wahrscheinlichkeiten

Inhalt dieser Seite

Einführung


Wiedergabe stellt eine Verbindung zu YouTube her.

Die eingehenden Emails in unserem Konto werden durch einen Spamfilter vorsortiert.

Bedingte Wahrscheinlichkeiten sind uns bei der Betrachtung von Baumdiagrammen schon begegnet, wir haben sie dort nur noch nicht so genannt. Wir führen sie hier aber dennoch ganz von vorne und Schritt für Schritt ein.

Neben Baumdiagrammen sind Vierfeldertafeln eine weitere Möglichkeit, Daten übersichtlich darzustellen. Als Beispiel sehen wir uns die Verteilung der Schülerinnen und Schüler einer Stufe in den Mathe-GKs dem LK an:

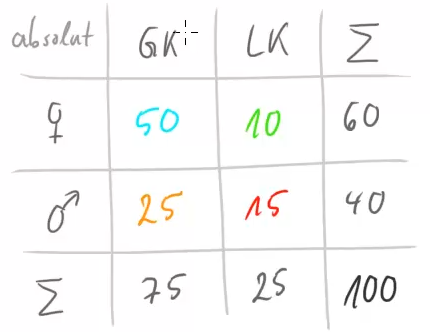
Eine Vierfeldertafel
Übersicht der Daten mithilfe einer Vierfeldertafel

Wir sehen hier, dass in den GKs insgesamt 50 Schülerinnen und 25 Schüler sind. Im LK sind es 10 Schülerinnen und 15 Schüler.
Das \Sigma („Sigma“) ist das Zeichen für „Summe“. In der entsprechenden Zeile bzw. Spalte steht also jeweils die Gesamtzahl.

In dieser ersten Vierfeldertafel haben wir die absoluten Anzahlen betrachtet. Stattdessen kann man aber auch die relativen Anzahlen oder auch Anteile betrachten:

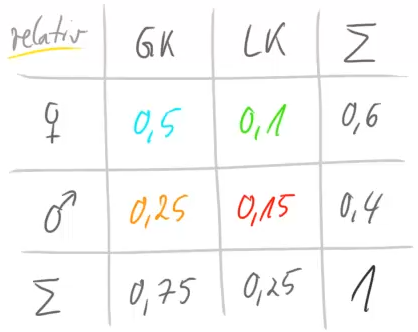
Vierfeldertafel mit relativen Angaben
Die Anteile der verschiedenen Schülergruppen

So die bei den relativen Häufigkeiten erhalten wir sie, indem wir einfach die Anzahlen durch die Gesamtzahl (in diesem Fall 100) teilen.

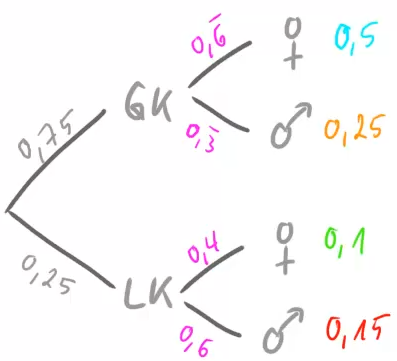
Es bietet sich nun an, diese Zahlen in einem Baumdiagramm darzustellen:

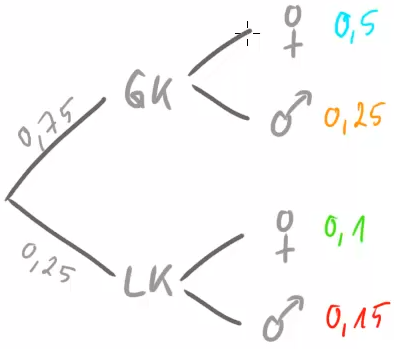
Ein Baumdiagramm1. Stufe GK/LK. 2. Stufe weiblich/männlich.
Die Anteile können wir auch in einem Baumdiagramm darstellen.

Machen wir uns noch einmal klar, welche Bedeutungen die Zahlen im Diagramm haben. Wir können sie einerseits als relative Häufigkeiten interpretieren aber andererseits auch als Wahrscheinlichkeiten.
Wählen wir zufällig eine Person aus dieser Stufe aus, dann ist die mit einer Wahrscheinlichkeit von 0{,}75 in einem Mathe-GK und mit einer Wahrscheinlichkeit von 0{,}25 im Mathe-LK:

    \[P(\mbox{GK}) = 0{,}75, \quad P(\mbox{LK}) = 0{,}25\]

Die Zahlen ganz rechts können wir so interpretieren:

    \begin{align*} P(\mbox{GK und w}) &= 0{,}5\\ P(\mbox{GK und w}) &= 0{,}25\\ P(\mbox{LK und w}) &= 0{,}1\\ P(\mbox{LK und m}) &= 0{,}15 \end{align*}

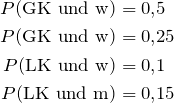
D.h. zum Beispiel, dass unsere zufällig gewählte Person mit einer Wahrscheinlichkeit von 0{,}5 weiblich und in einem GK ist.

In unserem Diagramm fehlen allerdings noch ein paar Zahlen. Die Beschriftungen der 2. Stufe fehlen, da wir die zugehörigen Werte nicht im der Vierfeldertafel vorfinden.
Diese fehlen Zahlen lassen sich aber recht leicht berechnen. Wir müssen lediglich die Wahrscheinlichkeit ganz rechts (z.B. 0{,}5) durch die Wahrscheinlichkeit der 1. Stufe (z.B. 0{,}75) teilen:

Das vollständige Baumdiagramm
Das vollständige Baumdiagramm

Diese von uns ergänzten Zahlen sind Beispiele für bedingte Wahrscheinlichkeiten. Warum man sie so nennt, wird uns klar, wenn wir uns deren Bedeutung bewusst machen.
Wenn wir nur aus den Schülerinnen und Schülern der GKs zufällig einen wählen, dann ist dieser mit einer Wahrscheinlichkeit von 0{,}\overline{6} weiblich und mit einer Wahrscheinlichkeit von 0{,}\overline{3} männlich.
Wenn wir hingegen nur aus den Schülerinnen und Schülern des LK zufällig einen wählen, dann ist dieser mit einer Wahrscheinlichkeit von 0{,}4 weiblich und mit einer Wahrscheinlichkeit von 0{,}6 männlich.

Dass wir diese unterschiedlichen Gruppen betrachten, schreiben wir so:

    \begin{align*} P_{\textrm{GK}}(\textrm{w}) &=0{,}\overline{6}\\ P_{\textrm{GK}}(\textrm{m}) &=0{,}\overline{3}\\ P_{\textrm{LK}}(\textrm{w}) &= 0{,}4\\ P_{\textrm{LK}}(\textrm{m}) &= 0{,}6 \end{align*}

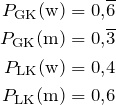
Die Bedingung, dass wir nur die GKs oder nur den LK betrachten, schreiben wir klein direkt unten an das P.

Umgekehrte Baumdiagramme


Wiedergabe stellt eine Verbindung zu YouTube her.

In unserem Baumdiagramm von oben haben wir in der 1. Stufe zwischen männlich und weiblich unterschieden und in der 2. Stufe zwischen GK und LK. Wir hätten aber ebenso diese beiden Merkmale in umgekehrter Reihenfolge betrachten können:

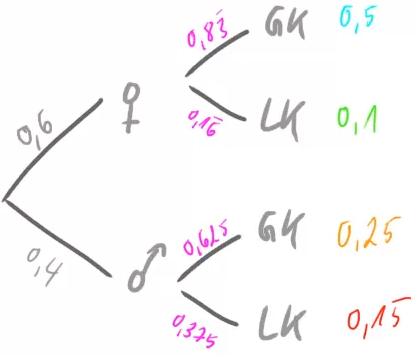
In diesem Baumdiagramm betrachten wir die Merkmale in umgekehrter Reihenfolge.
In diesem Baumdiagramm betrachten wir die Merkmale in umgekehrter Reihenfolge.

Die Anteile von männlichen und weiblichen Schülern und die Zahlen ganz rechts entnehmen wir wieder sofort der Vierfeldertafel. Die vier bedingten Wahrscheinlichkeiten

    \begin{align*} P_{\textrm{m}}(\textrm{GK}) &= \frac{0{,}5}{0{,}6} =0{,}8\overline{3}\\ P_{\textrm{m}}(\textrm{LK})&= \frac{0{,}1}{0{,}6} =0{,}1\overline{6}\\ P_{\textrm{w}}(\textrm{GK})&= \frac{0{,}25}{0{,}4} = 0{,}625\\ P_{\textrm{w}}(\textrm{LK})&= \frac{0{,}15}{0{,}4} = 0{,}375 \end{align*}

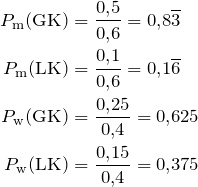
berechnen wir anschließend wieder, indem wir die Zahl ganz rechts durch die in der 1. Stufe teilen.

Stellen wir noch einmal das erste Baumdiagramm und das umgekehrte Baumdiagramm gegenüber:

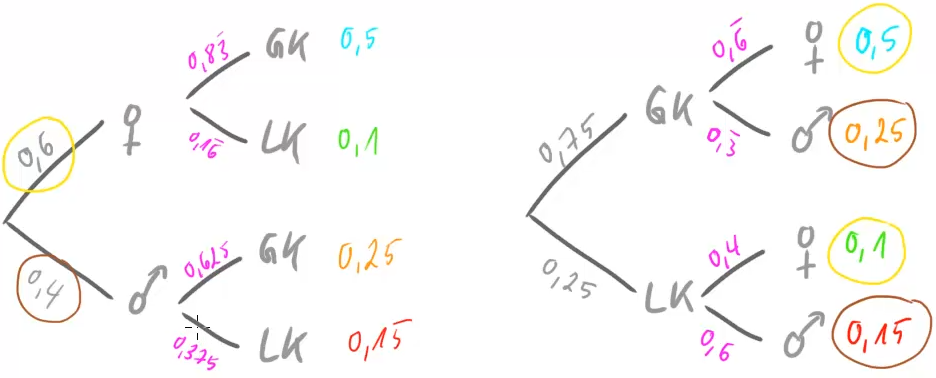
Beide Baumdiagramme im Vergleich
Beide Baumdiagramme im Vergleich

Beide Baumdiagramme enthalten zwar dieselben Informationen, allerdings sind die bedingten Wahrscheinlichkeiten, die man unmittelbar ablesen kann, verschieden. Daher ist es in vielen Situationen wichtig, zunächst zu überlegen, welches der beiden Diagramme man anfertigen sollte.

Möchten wir aus einem Baumdiagramm das umgekehrte erstellen, kann es hilfreich sein, als Zwischenschritt eine Vierfeldertafel anzufertigen (falls diese nicht ohnehin schon vorliegt). Möchten wir diesen Schritt vermeiden, können wir die Zahlen ganz rechts einfach übernehmen, wobei wir aufpassen müssen, welcher Wert zu welchem Pfad gehört. Die Wahrscheinlichkeiten der 1. Stufe erhalten wir mit der Pfadadditionsregel. Z.B. finden wir im rechten Baumdiagramm P(\textrm{w}) durch diese Rechnung:

    \[P(\textrm{w}) = P_{\textrm{GK}}(\textrm{w}) +P_{\textrm{LK}}(\textrm{w}) \]

Die zugehörigen Werte sind in der Abbildung gelb eingekreist.

Definition von bedingter Wahrscheinlichkeit


Wiedergabe stellt eine Verbindung zu YouTube her.

Mithilfe der Baumdiagramme haben wir gelernt, was unter bedingten Wahrscheinlichkeiten im Sachkontext zu verstehen ist. Zum Beispiel ist P_{\textrm{GK}}(\textrm{w}) die Wahrscheinlichkeit dafür, dass man bei zufälliger Wahl eines Mathe-GKlers eine Schülerin erwischt. Im Baumdiagramm haben wir diese Wahrscheinlichkeit so berechnet:

    \[P_{\textrm{GK}}(\textrm{w}) = \frac{P(\textrm{w und GK})}{P(\textrm{GK})} \]

Genau diese Rechnung steht Modell für die allgemeine Definition / Regel:

Die bedingte Wahrscheinlichkeit P_\textrm{A}(B), dass Ereignis B eintritt, unter der Voraussetzung, dass A bereits eingetreten ist, ist gegeben durch P_\textrm{A}(B) =\frac{P(\textrm{A und B})}{P(\textrm{A})}.

Statt „und“ verwendet man oft auch das Symbol \cap für Ereignisse. Dies ist möglicherweise auch beim im Unterricht verwendeten Buch der Fall. Dieses Zeichen stammt aus der Mengenlehre.

Stochastische Unabhängigkeit

Einführung


Wiedergabe stellt eine Verbindung zu YouTube her.

Manchmal fragt man sich, ob bei einem mehrstufigen Zufallsexperiment das Ergebnis in der 1. Stufe den weiteren Verlauf beeinflussen kann. Sehen wir uns ein Beispiel an, bei dem dies deutlich wird:

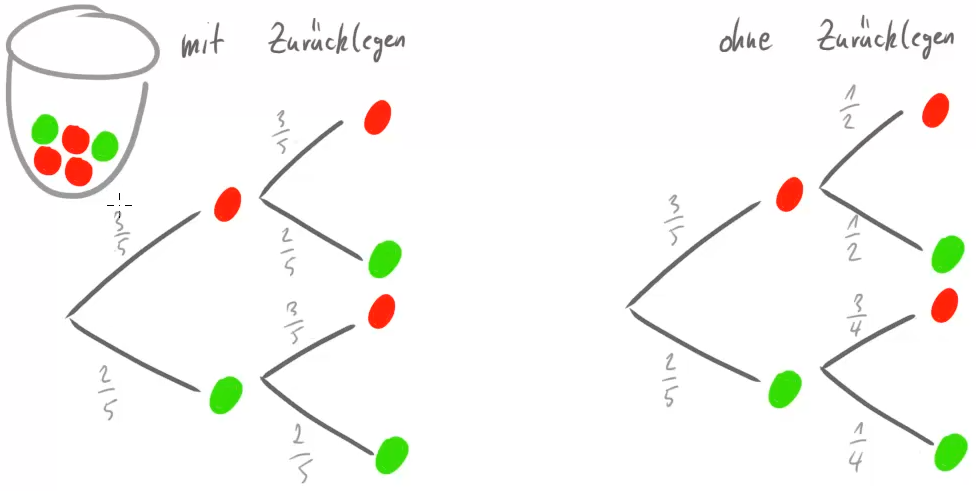
Ziehen aus einer Urne – mal mit mal ohne Zurücklegen
Ziehen aus einer Urne – mal mit mal ohne Zurücklegen

Wir betrachten eine Urne mit 2 grünen und 3 roten Kugeln. Aus dieser werden 2 Kugeln gezogen.

Legen wir die erste Kugel wieder zurück, dann hat die erste Kugel natürlich keinen Einfluss auf die Wahrscheinlichkeiten beim zweiten Ziehen. Legen wir sie aber nicht zurück, dann hat die erste Kugel sehr wohl einen Einfluss. Das sehen wir daran, dass die Wahrscheinlichkeiten in der 2. Stufe im rechten Diagramm verschieden sind, je nachdem ob zuerst Rot oder zuerst Grün gezogen wurde.

Bei diesem Beispiel war es von vorneherein klar, ob das Ergebnis der 1. Stufe die 2. Stufe beeinflusst. In vielen Situationen ist dies aber gar nicht klar, sondern kann erst anhand von gegebenen Zahlen berechnet werden.
Nehmen wir dazu an, wir wollen prüfen, ob die Wahl eines LKs vom Sternzeichen Löwe abhängt. Das ist etwas absurd, soll aber deutlich machen, dass dies mit Logik allein nicht zu begründen wäre – wir brauchen Daten, mit denen wir rechnen können.
Die Auswertung an einer Schule hat vielleicht dies hier ergeben:

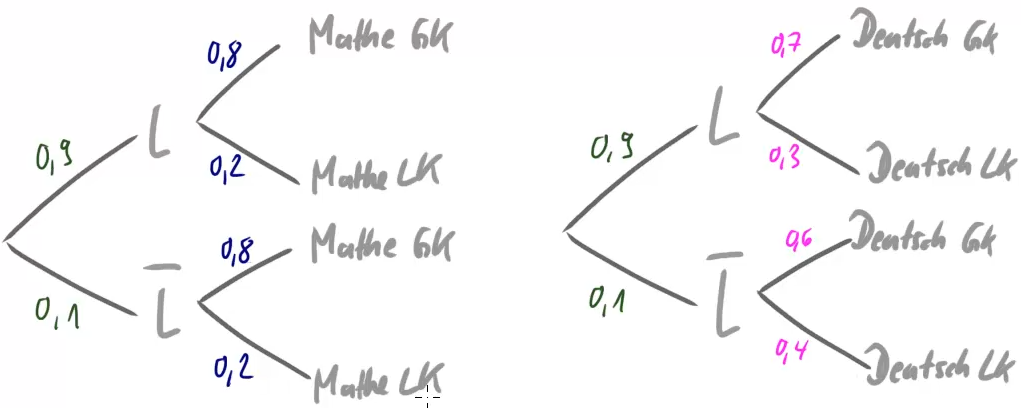
Zwei Baumdiagramme
Beeinflusst das Sternzeichen Löwe (L) die Wahl eines LKs?

Das L steht dabei für „Sternzeichen Löwe“. Hier ist es so, dass die Wahl eines Mathe-LKs nicht von diesem Sternzeichen abhängt. Die Wahl eins Deutsch-LKs hingegen schon.

Man sagt, dass die Merkmale Sternzeichen Löwe und Mathe-LK stochastisch unabhängig voneinander sind. Die Merkmale Sternzeichen Löwe und Deutsch-LK sind aber stochastisch abhängig voneinander.

Formale Definition


Wiedergabe stellt eine Verbindung zu YouTube her.

In der Stufe 10 und oder in einem Grundkurs dürfte die Erklärung von oben, was unter stochastischer Unabhängigkeit zu verstehen ist, eigentlich genügen.
Für alle, die etwas neugieriger sind, sehen wir uns noch etwas striktere und formalere Definition an:

Zwei Ereignisse A und B heißen stochastisch unabhängig voneinander, falls P(A \cap B) = P(A) \cdot P(B).

Mit der folgenden Überlegung können wir uns einen groben Eindruck davon machen, warum dies eine geeignete formale Definition ist.
Wir gehen zunächst davon aus, dass P(A) > 0 ist, d.h., Ereignis A ist nicht das unmögliche Ereignis. Sind nun A und B stochastisch unabhängig voneinander, gilt P(A \cap B) = P(A) \cdot P(B), was wir umformen können zu P(B) = \frac{P(A \cap B)}{A}.
Der Bruch \frac{P(A \cap B)}{A} ist aber genau die bedingte Wahrscheinlichkeit P_A(B). D.h., wir erhalten insgesamt P(B) = P_A(B). Das Eintreten von A verändert also die Wahrscheinlichkeit für das Eintreten von B nicht, wenn wir stochastische Unabhängigkeit im Sinne der formalen Definition voraussetzen. Mit ein paar weiteren Umformungen kann man auch zeigen, dass dann auch P_{\overline{A}}(B)=P(B) gilt. Das spiegelt genau unsere Einführung von oben wieder, in der wir gesagt haben, dass die Teilbäume der zweiten Stufe gleich beschriftet sein müssen.

Der Satz von Bayes


Wiedergabe stellt eine Verbindung zu YouTube her.

Nehmen wir an, wir haben ein Baumdiagramm gegeben und kennen alle Wahrscheinlichkeiten, die man dort angeben kann:

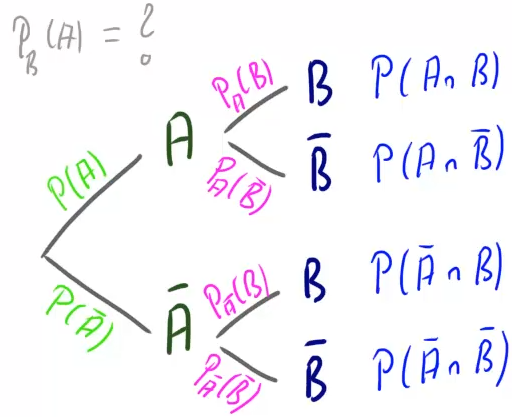
Ein gewöhnliches Baumdiagramm.
Viele Wahrscheinlichkeiten kann man hier ablesen – aber nicht alle!

Wir möchten aber leider die bedingte Wahrscheinlichkeit P_B(A) bestimmen, die ausgerechnet nicht in diesem Baumdiagramm zu finden ist, sondern nur im umgekehrten.

Der Satz von Bayes, den wir nun herleiten, liefert uns eine Formel, diese Wahrscheinlichkeit aus den gegebenen Wahrscheinlichkeiten zu berechnen ohne das gesamte umgekehrte Baumdiagramm zu erstellen.

Um den Satz aber erst einmal herzuleiten, müssen wir uns nochmal das umgekehrte Baumdiagramm vor Augen führen:

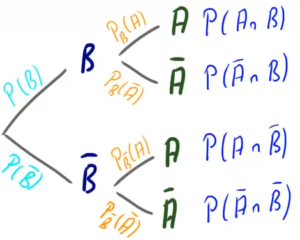
Ein umgekehrtes Baumdiagramm

Die gesuchte Wahrscheinlichkeit steht ganz oben an der 2. Stufe. Würden wir das Baumdiagramm erstellen, würden wie sie berechnen durch: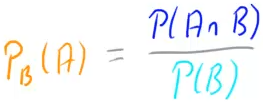
P_B(A)=(PA und B) / P(B)Die Wahrscheinlichkeit P(B) müssen wir beim umkehren des Baumdiagramm aber auch zunächst bestimmen, indem wir die Wahrscheinlichkeiten der zwei Pfade im ursprünglichen Diagramm, die in B enden addieren:
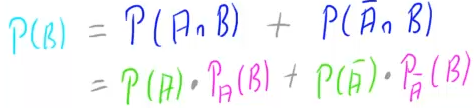Rechnung, die zu P(B) führtFügen wir nun die beide Gleichungen zusammen, erhalten wir den Satz von Bayes:
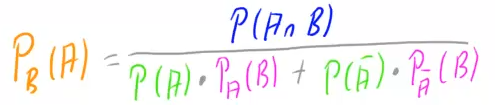Satz von BayesLetztlich stellt er eigentlich nur eine Zusammenfassung der Rechnung dar, die man automatisch durchführt, wenn man das umgekehrte Baumdiagramm erstellt.

Übungsaufgabe


Wiedergabe stellt eine Verbindung zu YouTube her.

Die eingehenden Emails in einem Konto werden durch einen Spamfilter in die beiden Ordner „verdächtig“ und „Eingang“ vorsortiert. Wir betrachten die folgenden Ereignisse:

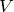  • V: Eine Email landet im Ordner „verdächtig“.
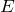  • E: Eine Email landet im Ordner „Eingang“.
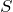  • S: Eine Email ist tatsächlich Spam.
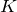  • K: Eine Emal ist kein Spam.

Die im Baumdiagramm gegebenen Wahrscheinlichkeiten sind bekannt: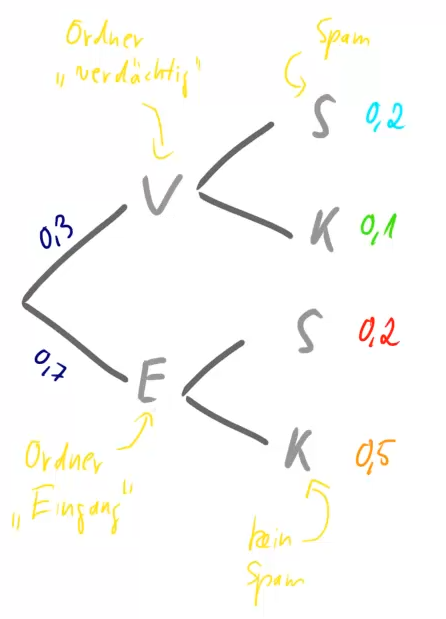
Baumdiagramm mit 2 Stufen

  1. Berechne die fehlenden Werte in diesem Diagramm.
  2. Bestimme mit dem Satz von Bayes P_S(V).
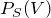  3. Erstelle das umgekehrte Baumdiagramm.
  4. Stelle die zugehörige Vierfeldertafel auf.
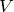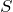  5. Ermittle, ob V und S voneinander stochastisch unabhängig sind.

Die Lösungen gibt es im Clip!