Grundbegriffe – Dr. Daniel Appel

Inhalt dieser Seite

Zufallsversuch, Ergebnis und Ereignis
Elementare Summenregel und Komplementärregel
Laplace-Versuche
Absolute und relative Häufigkeit
Empirisches Gesetz der großen Zahlen
Würfel haben kein Gedächtnis

Zufallsversuch, Ergebnis und Ereignis

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

In der Stochastik untersuchen wir sogenannte Zufallsversuche (oder auf Zufallsexperimente). Das sind Versuche, deren Ergebnis durch einen Zufall bestimmt wird.
Zu jedem Zufallsversuch gehört eine Ergebnismenge, die häufig mit $S$ bezeichnet wird. Diese Menge gibt alle erdenklichen Ergebnisse des Versuchs an.

Hier ein paar Beispiele:

Zufallsversuch	Ergebnismenge
Werfen eines Würfels	$S=\{1, 2, 3, 4, 5, 6\}$
Werfen zweier Würfel	$S=\{(1,1), (1,2), \dots, (6,6)\}$
Ziehen einer Spielkarte	$S=\{\mbox{Herz-As},\mbox{Herz-König}, \dots,\mbox{Kreuz-7}\}$

Aus den Ergebnissen können wir uns Ereignisse konstruieren, oder umgekehrt ausgedrückt, ein Ereignis besteht aus Ergebnissen.
Beim einfachen Würfelwurf können wir zum Beispiel das Ereignis $U$ betrachten, das angibt, dass eine ungerade Zahl gewürfelt wird. Dann besteht $U$ aus den Ergebnissen $1$ , $3$ und $5$ , d.h., $U=\{1, 3, 5\}$ .
Beim Werfen zweier Würfel könnten wir das Ereignis $G$ betrachten, das aus den Ergebnissen besteht, in denen bei beiden Würfeln die gleiche Zahl fällt:

$G=\{(1,1), (2,2), (3,3), (4,4), (5,5), (6,6) \}$

Wir werden häufig versuchen, die Wahrscheinlichkeiten für verschiedene Ereignisse zu berechnen. Die Wahrscheinlichkeit eines Ereignisses $E$ schreibt man als $P(E)$ , also zum Beispiel $P(U)=\frac{1}{2}$ für das Ereignis $U$ von oben.

Elementare Summenregel und Komplementärregel

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

Die elementare Summenregel sagt folgendes aus. Falls ein Ereignis $E$ aus den Ergebnissen $e_1$ , $e_2$ ,…, $e_n$ besteht, dann müssen wir einfach die Wahrscheinlichkeiten der einzelnen Ergebnisse addieren, um $P(E)$ zu berechnen:

$P(E) = P(e_1) + P(e_2) + \cdots + P(e_n)$

Beim Werfen eines Würfels hat zum Beispiel jedes Ergebnis die Wahrscheinlichkeit $\frac{1}{6}$ . Deswegen können wir $P(U)$ so berechnen:

$P(U) = P(1) + P(3) + P(5) =\frac{1}{6} +\frac{1}{6} +\frac{1}{6} = \frac{3}{6} = \frac{1}{2}$

Nehmen wir als weiteres Beispiel beim einfachen Würfelwurf das Ereignis $A = \{1, 2, 3\}$ , das besagt, dass eine Zahl kleiner oder gleich $3$ geworfen wird. Auch $A$ hat die Wahrscheinlichkeit $\frac{1}{2}$ .

Wenn wir mit den Ereignissen $U$ und $A$ weiterrechnen wollen, müssen wir aufpassen. Man könnte ja denken, dass die Wahrscheinlichkeit dafür, dass wenigstens eines der Ereignisse $U$ oder $A$ eintritt – also dass eine der Zahlen $1$ , $2$ , $3$ , $5$ fällt – auch einfach die Summe der einzelnen Wahrscheinlichkeiten $P(U)$ und $P(A)$ ist.
Das ist aber nicht so! Die Wahrscheinlichkeit, dass eine dieser Zahlen fällt, ist $\frac{4}{6}$ , aber $P(U)+P(A) = 1$ .
Diese Rechnung geht schief, weil wir die elementare Summenregel nur benutzen dürfen, um Wahrscheinlichkeiten von Ergebnissen zu addieren. Dadurch, dass die Ergebnisse $1$ und $3$ in $U$ und in $A$ stecken, kommt hier eine falsche Wahrscheinlichkeit heraus.

Zu jedem Ereignis $E$ gibt es auch das sogenannte Gegenereignis $\overline{E}$ . Diese besteht aus den Ergebnissen, die nicht in $E$ liegen.
Zum Beispiel gilt $\overline{U} = \{2, 4, 6\}$ .

Die gesamte Ergebnismenge $S$ wird also aufgeteilt in $E$ und $\overline{E}$ , d.h., jedes Ergebnis kommt in einem der beiden (aber nicht in beiden!) Ereignissen vor. Deswegen muss gelten $P(E) + P(\overline{E}) = 1$ oder anders ausgedrückt:

$P(E) = 1 - P(\overline{E})$

Dies ist die Komplementärregel.

Aufgrund der elementaren Summenregel, ist es oft schlau, zu versuchen, die Wahrscheinlichkeiten für die Ergebnisse zu bestimmen. Kennen wir alle diese Wahrscheinlichkeiten, können wir für jedes Ereignis die Wahrscheinlichkeit berechnen.
Manchmal ist das Gegenereignis $\overline{E}$ einfacher zu verstehen als $E$ selbst. Dann kann es klug sein, zuerst $P(\overline{E})$ zu bestimmen und dann einfach die Komplementärregel $P(E) = 1 -P(\overline{E})$ zu benutzen.

Laplace-Versuche

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

Laplace-Versuche sind eine besonders einfache Art von Zufallsversuchen. Man nennt einen Zufallsversuch, Laplace-Versuch, falls alle Ergebnisse dieselbe Wahrscheinlichkeit haben.

Ein Beispiel für einen Laplace-Versuch ist das Werfen eines Würfels. Hier hat jede Zahl dieselbe Wahrscheinlichkeit.
Wäre der Würfel jedoch gezinkt, so dass z.B. die $6$ eine höhere Wahrscheinlichkeit besitzt, wäre dies kein Laplace-Versuch mehr.

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

Da bei einem Laplace-Versuch jedes Ergebnis dieselbe Wahrscheinlichkeit besitzt, ist es leicht, diese Wahrscheinlichkeit zu bestimmen. Zum Beispiel hat beim Würfelwurf jede Zahl die Wahrscheinlichkeit $\frac{1}{6}$ , da es sechs Zahlen gibt. Allgemein gilt folgende Regel:

Bei einem Laplace-Versuch mit $n$ verschiedenen Ergebnissen hat jedes Ergebnis die Wahrscheinlichkeit $\frac{1}{n}$ .

Mithilfe dieser Regel ist es auch leicht, die Wahrscheinlichkeit für Ereignisse zu bestimmen. Wir müssen nämlich nur zählen, wie viele Ergebnisse zu dem Ereignis gehören. Unser Ereignis $U =\{1, 3, 5 \}$ , das wir oben schon betrachtet haben, besteht aus drei Ergebnissen. Da jedes davon die Wahrscheinlichkeit $\frac{1}{6}$ hat, besitzen sie zusammen die Wahrscheinlichkeit $\frac{3}{6}$ . Allgemein gilt:

Laplace-Regel: Betrachten wir einen Laplace-Versuch mit $n$ Ergebnissen und ein Ereignis zu dem $k$ Ergebnisse gehören, dann hat das Ereignis die Wahrscheinlichkeit $\frac{k}{n}$ . Oder in Worten: „Anzahl zugehöriger Ergebnisse durch Anzahl aller Ergebnisse.“

Absolute und relative Häufigkeit

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

Stellen wir uns vor, wir werfen einen Würfen 100 mal und zählen, wie oft die verschiedenen Ergebnisse vorliegen:

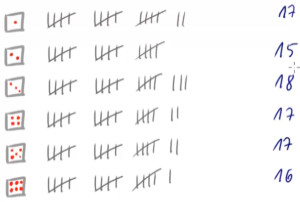
Strichliste zum Zählen der Egebnisse — Die absoluten Häufigkeiten der Ergebnisse erhalten wir durch Zählen.

Dann haben wir nichts anderen getan, als die absoluten Häufigkeiten der Ergebnisse in diesem Zufallsversuch zu ermitteln. Diese absoluten Häufigkeiten sind nämlich genau diese Anzahlen.

Die relative Häufigkeit eines Ergebnisses erhalten wir, wenn wir die absolute Häufigkeit durch die Anzahl der Versuche teilen:

$\mbox{relative Häufigkeit} = \frac{\mbox{absolute Häufigkeit}}{\mbox{Gesamtzahl der Versuche}}$

In der Abbildung wurde der Würfel insgesamt 100 mal geworfen. Mit den Zahlen von oben können wir diese Tabelle erstellen:

Ergebnis	absolute Häufigkeit	relative Häufigkeit
$1$	$17$	$\frac{17}{100}$
$2$	$15$	$\frac{15}{100}$
$3$	$18$	$\frac{18}{100}$
$4$	$17$	$\frac{17}{100}$
$5$	$17$	$\frac{17}{100}$
$6$	$16$	$\frac{16}{100}$

Wozu gibt es nun diese beiden Arten von Häufigkeiten?
Die absolute Häufigkeit verrät uns unmittelbar, wie oft ein Ergebnis eingetreten ist. Allerdings gibt Sie uns kein Gefühl dafür, ob das Ergebnis damit eine große oder kleine Wahrscheinlichkeit hat. Erst wenn wir wie bei der relativen Häufigkeit die Gesamtzahl ins Spiel bringen, sehen wir, ob ein Ergebnis eher häufig oder eher selten eingetreten ist.
Die relative Häufigkeit alleine sagt uns aber nicht mehr, wie oft ein Ergebnis eintrat. Wenn ich z.B. sage, ich hätte mehrfach einen Würfel geworfen und die relative Häufigkeit der $6$ war $\frac{1}{2}$ , ist überhaupt nicht erkennbar, wie viele Würfe ich gemacht habe.

Empirisches Gesetz der großen Zahlen

Dieses Video auf YouTube ansehen

Wiedergabe stellt eine Verbindung zu YouTube her.

Wie oben schon erwähnt, geben uns die relativen Häufigkeiten ein Gefühl dafür, wie häufig ein Ergebnis vorkommt. Je öfter wir einen Zufallsversuch wiederholen, desto besser helfen uns die relativen Häufigkeiten, die Wahrscheinlichkeiten für die Ergebnisse abzuschätzen.

Sehen wir uns ein Beispiel an. Ein Würfel wurde 10 mal geworfen. Die Ergebnisse sind in dieser Tabelle notiert:

Absolute und relative Häufigkeiten beim zehnfachen Würfelwurf. Entnommen aus meinem Clip.

Wie wir in dieser Tabelle vielleicht sehen, sind 10 Würfe viel zu wenig, um einen Eindruck davon zu bekommen, wie groß die Wahrscheinlichkeiten für die verschiedenen Ergebnisse sind. In diesen 10 Würfen trat z.B. die $5$ noch nicht auf. Es könnte der falsche Eindruck entstehen, die Wahrscheinlichkeit für sie wäre $0$ .

Also werfen wir den Würfel noch häufiger:

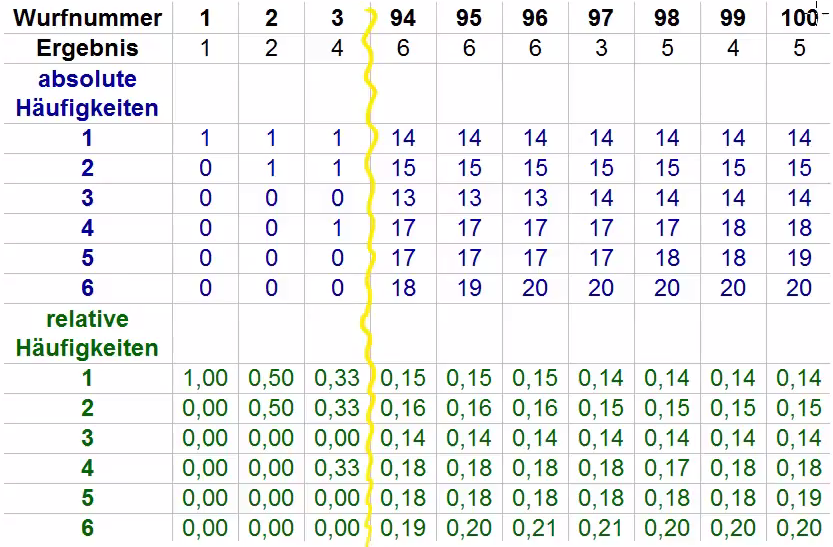
Nun wurde 100 mal geworfen. Die Tabelle stammt wieder aus meinem Clip.

Nach 100 Würfen kamen alle Zahlen zwischen $14$ und $20$ mal vor. Es ist aber immer noch nicht erkennbar, ob einige Zahlen wahrscheinlicher sind als andere.

Werfen wir insgesamt 500 mal:

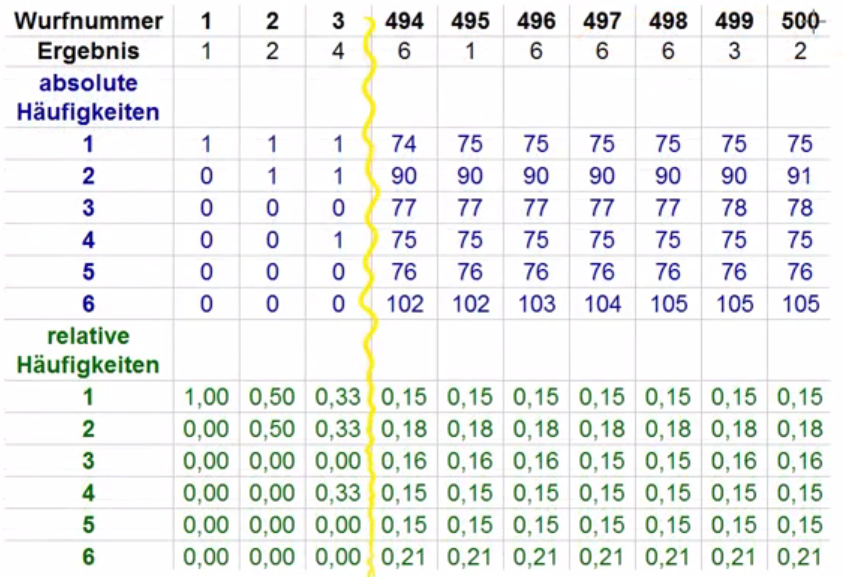
Nun sehen wir, dass die relativen Häufigkeiten im Vergleich zu vorher ausgeglichener sind. Jedoch kommt die $6$ ungewöhnlich oft vor.

Würden wir noch häufiger Werfen, sollten wir einen immer besseren Ausgleich feststellen. Sollte die $6$ nach wie vor ungewöhnlich oft auftreten, könnte es aber auch sein, dass der Würfel gezinkt ist.

Die Tatsache, dass die relativen Häufigkeiten bei sehr vielen Wiederholungen immer näher an den tatsächlichen Wahrscheinlichkeiten liegen, nennt man empirisches Gesetz der großen Zahlen. Diese eigentliche recht simple Beobachtung kann sehr nützlich bei Zufallsversuchen sein, bei denen wir anders als beim Würfel die Wahrscheinlichkeiten der Ergebnisse noch nicht kennen.

Ein klassisches Beispiel ist das Werfen einer Reißzwecke. Wie wahrscheinlich ist es wohl, dass sie mit der Spitze nach oben oder aber auf der Seite liegen bleibt?
Dies könnten wir abschätzen, indem wir eine Reißzwecke 100 oder auch 1000 oder 10000 mal werfen und die relativen Häufigkeiten bestimmen. Diese geben uns Abschätzungen für die tatsächlichen Wahrscheinlichkeiten.

Würfel haben kein Gedächtnis

Eine häufige Fehlinterpretation des empirischen Gesetzes der großen Zahlen ist, dass man glaubt, aufgrund der vorherigen Ergebnissen etwas über die zukünftigen sagen zu können. Zum Beispiel könnte man vielleicht denken, dass die $6$ bei unserem Würfel von oben schon so oft kam, dass sie nun zum Ausgleich etwas seltener auftreten müsste. Das stimmt aber nicht! Die Wahrscheinlichkeit bleibt immer gleich!

Auch beim Lotto ist es z.B. nicht so, dass eine Zahl, die lange nicht gezogen wurde nun eine größere Chance hat zu fallen.

Dies fasst man gerne unter dem Spruch Würfel haben kein Gedächtnis zusammen.