Zufallsgrößen und Erwartungswerte

Inhalt dieser Seite

Einführung von Zufallsgrößen


Wiedergabe stellt eine Verbindung zu YouTube her.

Manchmal kann es nützlich sein, den Ergebnissen von Zufallsversuchen gewissen Zahlenwerte zuzuordnen.

Stellen wir uns z.B. eine Urne mit 2 grünen und 3 roten Kugel vor. Aus dieser soll eine Kugel gezogen werden. Wir haben also zwei mögliche Ergebnisse: Rot und Grün. Mit diesen beiden Farben ist es aber natürlich unpraktisch, weiter zu rechnen. Schließlich kann man ja nur mit Zahlen vernünftig rechnen.
Wenn wir Glück haben, dann können wir den beiden Farben aber in sinnvoller Weise Zahlenwerte zuordnen. Es könnte z.B. sein, dass es sich um ein Gewinnspiel handelt, bei dem man je nach gezogener Farbe einen anderen Gewinnbetrag ausgezahlt bekommt. Bei Rot könnte es 1 € und bei Grün 5 €.

Dieser Gewinn stellt nun eine Zufallsgröße dar. Anschaulich gesprochen, bedeutet das, dass der Gewinn ein Zahlenwert ist, der vom Zufall abhängt. Formal definiert man eine Zufallsgröße so:

Eine Zufallsgröße ist eine Funktion, die jedem Ergebnis eines Zufallsversuchs eine reelle Zahl zuordnet. Eine Zufallsgröße wird mit einem Großbuchstaben (z.B. X) bezeichnet.

Eine Zufallsgröße können wir uns oft als Tabelle veranschaulichen:

Ergebnis Zufallsgröße X: \mbox{Gewinn} Wahrscheinlichkeit
Rot 1 € \frac{3}{5}
Grün 5 €  \frac{2}{5}

Solche Zuordnungen gab es möglicherweise schon häufiger im Unterricht Erwähnung des Wortes „Zufallsgröße“. In manchem Mathebüchern der EF kommt es auch gar nicht vor.

Kommen wir zu noch einem Beispiel. Auch aus einem einfachen Würfelwurf können wir ein Glücksspiel konstruieren; bei einer 1 erhält man als Gewinn 10 €, bei einer 6 muss man einen Euro Strafe zahlen und bei allen anderen Zahlen erhält man einen Euro Gewinn:

Ergebnis Zufallsgröße X: \mbox{Gewinn} Wahrscheinlichkeit
1 10 € \frac{1}{6}
2 1 € \frac{1}{6}
3 1 € \frac{1}{6}
4 1 € \frac{1}{6}
5 1 € \frac{1}{6}
6 -1 € \frac{1}{6}

Bei diesem Beispiel sollte deutlich werden, dass die Zufallsgröße nicht unbedingt dasselbe ist wie das Ergebnis, auch wenn das Ergebnis selbst schon eine Zahl ist.

Wir könnten die Tabelle jetzt etwas vereinfachen:

Zufallsgröße X: \mbox{Gewinn} Wahrscheinlichkeit
10 € \frac{1}{6}
1 €  \frac{4}{6}
-1 €  \frac{1}{6}

Eine solche Tabelle nennt man übrigens auch Wahrscheinlichkeitsverteilung. Formal definiert man den Begriff Wahrscheinlichkeitsverteilung so:

Eine Funktion die jedem Wert einer Zufallsgröße X die zugehörige Wahrscheinlichkeit zuordnet, nennt man Wahrscheinlichkeitsverteilung.
Hat die Zufallsgröße X nur endlich viele Werte, kann man die Wahrscheinlichkeitsverteilung in einer Tabelle mit den Spalten „Zufallsgröße X“ und „Wahrscheinlichkeit“ darstellen.

Bei solchen Glücksspielen stellt sich natürlich die Frage, ob man daran teilnehmen sollte oder mit welchem Gewinn bzw. Verlust auf lange Sicht zu rechnen ist. Dies führt uns direkt zum nun folgenden Abschnitt.

Einführung des Erwartungswertes


Wiedergabe stellt eine Verbindung zu YouTube her.

Stellen wir uns vor, wir spielen das Glücksspiel mit der Urne 100 mal. Dann werden wir in etwa \frac{3}{5} der Fälle Rot und in etwa \frac{2}{5} der Fälle Grün ziehen. Mit anderen Worten, etwa 60 mal gewinnen wir 1 € und etwa 40 mal 5 €:
Ergebnis Zufallsgröße X Wahrscheinlichkeit Häufigkeit bei 100 Spielen Gesamtgewinn bei 100 Spielen
Rot 1 \frac{3}{5} ca. \frac{3}{5}\cdot 100 = 60 ca. 60 €
Grün 5 \frac{2}{5} ca. \frac{2}{5} \cdot 100 =40  ca. 200 €

Bei 100 Spielen dürfen wir also mit einem Gesamtgewinn von 260 € rechnen. Pro Spiel wären dass also im Mittel 2{,}60 €.
Diese 2{,}60 € sind der sogenannte Erwartungswert der Zufallsgröße X. Man schreibt kurz E(X)=2{,}60 €.

Den Erwartungswert hätten wir auch wesentlich kompakter berechnen können als mit dieser großen Tabelle oben:

    \[E(X) = \frac{3}{5} \cdot 1 + \frac{2}{5} \cdot 5 = 2{,}6\]

Wir müssen also immer die Wahrscheinlichkeit mit dem zugehörigen Wert der Zufallsgröße (also dem Gewinn) multiplizieren und diese Ergebnisse danach addieren.
Warum diese Rechnung funktioniert, wird im Clip näher erläutert!

Wir sollten nun aber die wichtigsten Punkte festhalten:

Der Erwartungswert E(X) einer Zufallsgröße X beschreibt den im Mittel zu erwartenden Wert von X bei einer hohen Anzahl von Wiederholungen des Zufallsversuchs.
Wenn der Zufallsversuch die Ergebnisse a_1, a_2 bis a_n hat, gilt:

    \[E(X)= a_1 \cdot P(X=a_1) + a_2\cdot P(X=a_2) + \cdots + a_n\cdot P(X=a_n)\]

Ist im Kontext klar, welche Zufallsgröße gemeint ist, schreibt man auch \mu anstatt E(X).

Beispiele zur Berechnung von Erwartungswerten


Wiedergabe stellt eine Verbindung zu YouTube her.

Zur Vertiefung sehen wir uns noch zwei Beispiele zur Bestimmung des Erwartungswertes einer Zufallsgröße an. In beiden Beispielen betrachten wir als Zufallsversuch das zweifache Werfen eines Würfels, jedoch untersuchen wir dann verschiedene Zufallsgrößen.

Zuerst betrachten wir die Zufallsgröße S, die die Summe der beiden gewürfelten Augenzahlen darstellt.
Um eine Übersicht über die auftretenden Summen und deren Wahrscheinlichkeiten zu erlangen, fertigen wir eine Tabelle an:

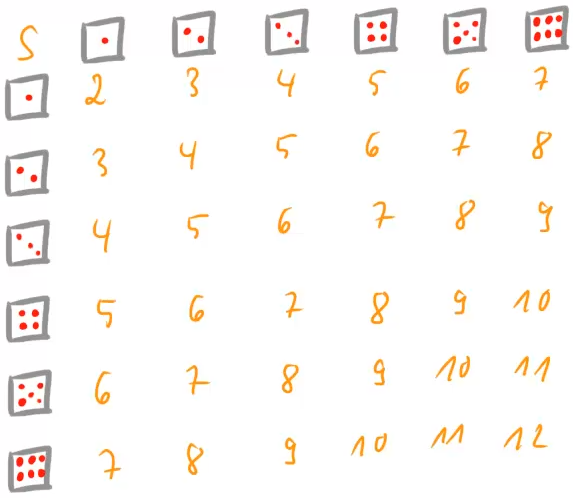
Die Summen der Augenzahlen beim zweifachen Würfelwurf.
Die Summen der Augenzahlen beim zweifachen Würfelwurf.

Wie uns eigentlich schon vorher klar gewesen sein dürfte, können als Summen die Zahlen 2 bis 12 auftreten. Nun sehen wir aber sehr schön, wie viele unterschiedliche Ergebnisse des zweifachen Würfelwurfs jeweils zu den verschiedenen Ergebnissen führen.