In der Logik (wie wir sie verwenden werden) kann man Aussagen oder auch Bedingungen miteinander verknüpfen. Stell Dir dazu vor, Du möchtest eine Bedingung dafür formulieren, ob Du heute Abend ins Kino gehst. Als Bedingung könnte man sich das hier vorstellen:
Es läuft ein guter Film.
Das alleine scheint aber vielleicht etwas grob zu sein, denn Deine Entscheidung hängt sicherlich noch von anderen Faktoren ab. Daher könntest Du sie mit einer weiteren Bedingung beispielsweise durch ein Und verknüpfen:
Es läuft ein guter Film und ein Freund hat Zeit mitzukommen.
Eine weitere denkbare Verknüpfung wäre diese mit einem Oder:
Es läuft ein guter Film oder ein Freund hat Zeit mitzukommen.
Sehen wir uns in der folgenden Tabelle an, in welchen Fällen Du ins Kino gehen würdest, wenn Du Dich ganz strikt an die Bedingung mit Und bzw. mit Oder hältst:
| Läuft ein guter Film? | Hat ein Freund Zeit mitzukommen? | Und | Oder |
| nein | nein | nein | nein |
| nein | ja | nein | ja |
| ja | nein | nein | ja |
| ja | ja | ja | ja |
Bei der Verknüpfung mit Und gehst Du nur ins Kino, wenn beide Bedingungen erfüllt sind. Bei der mit Oder genügt es schon, dass eine Bedingung erfüllt ist.
Das Und und das Oder kannst Du Dir wie zwei Grundrechenarten in der Logik vorstellen. Neben diesen beiden gibt es aber noch das nicht, oder wie man auch sagt die Negation. Wir können damit zum Beispiel die beiden Einzelbedingungen
Es läuft ein guter Film.
und
Morgen schreiben wir eine Klassenarbeit.
verknüpfen zu
Es läuft ein guter Film und morgen schreiben wir nicht eine Klassenarbeit.
Oft kürzt man die Formulierung von Verknüpfungen ab, indem man den einzelnen Bedingungen Namen gibt. Zum Beispiel:
A: Es läuft ein guter Film.
B: Ein Freund hat Zeit mitzukommen.
Statt beispielsweise
Es läuft ein guter Film und ein Freund hat Zeit mitzukommen.
schreibt man dann kurz
A und B.
Als weiteres Beispiel könnte man auch „nicht B“ schreiben, um „Kein Freund hat Zeit mitzukommen.“ auszudrücken. Die Negation ist hier in dem Wort „Kein“ versteckt.
Um noch mehr Schreibarbeit zu sparen, schreibt man gerne statt „Ja“ eine 1 und statt „Nein“ eine 0.
Übung
Gegeben sind zwei Bedingungen, die wir mit A und B bezeichnen. Wie diese aussehen, soll egal sein. Es geht nur um die formalen Verknüpfungen.
Ergänze die folgende Tabelle.
| Ist A erfüllt? | Ist B erfüllt? | A und nicht B | A oder nicht B | A und nicht B |
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
Kniffelige logische Verknüpfungen kann man auch mithilfe einer Zeichnung untersuchen, die sehr stark an einen Rechenbaum aus der Grundschule erinnert:
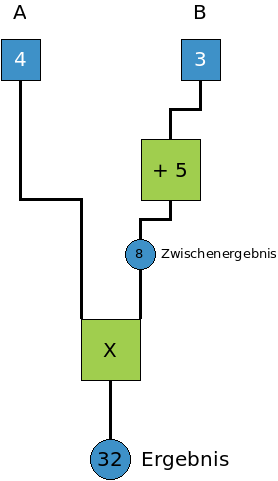
Bei diesem Rechenbaum kann man für A und B jeweils eine Zahl einsetzen. Im Rechenbaum wird dann A×(B+5) berechnet, also wie zum Beispiel in der Abbildung 4×(3+5) = 4×8 = 32.
Sehen wir uns nun an, wie man logische Verknüpfungen mit einem Rechenbaum – oder vielleicht eher „Logikbaum“ – darstellen kann. Beispielsweise könnten wir
A und nicht B
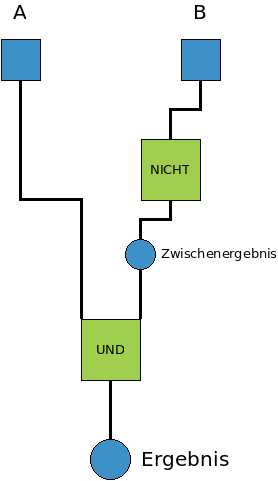
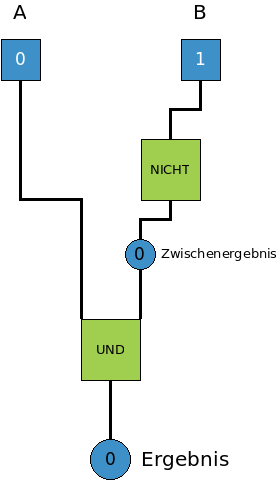
mithilfe eines Rechenbaumes so darstellen:
Eine Beispielrechnung sehen wir hier:Man kann logische Verknüpfungen so wie Rechnungen in der Mathematik durch Klammern strukturieren. Außerdem gibt es wie in der Mathematik auch noch weitere Vorfahrtsregeln. Zum Beispiel geht nicht immer vor Und und Oder. D.h. zum Beispiel, dass „nicht A und B“ gleichbedeutend ist mit „(nicht A) und B“. Aber diese Regeln werden wir an dieser Stelle nicht weiter vertiefen, sondern nur so weit ansehen, wie wir sie jeweils benötigen.
Hier die Videoversion dieses Abschnitts:
Wiedergabe stellt eine Verbindung zu YouTube her.