Einführung
Binärbäume unterscheidet sich von den Datenstrukturen die wir bisher betrachtet haben in einem wesentlichen Punkt: Die Objekte sind nicht mehr linear angeordnet.
Bevor wir aber damit beginnen, Objekte in Bäumen abzulegen, betrachten wir erst einmal die Struktur dieser Binärbäume an sich.
Formal kann man Binärbäume wie folgt definieren:
| Ein Binärbaum kann leer sein. Ist er nicht leer, dann besitzt er einen Knoten, der als Wurzel bezeichnet wird. Mit dieser Wurzel verbunden sind durch sogenannte Kanten sein linker und sein rechter Teilbaum, die wiederum Binärbäume sind. |
Dazu hier ein Beispiel:
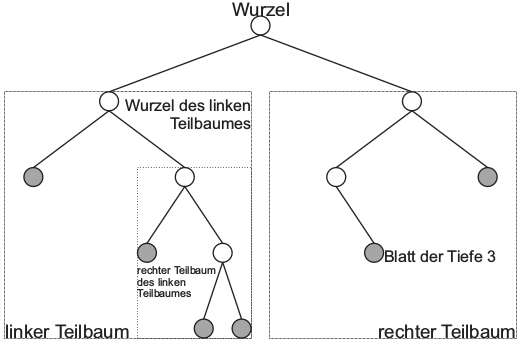
Die grau markierten Knoten in obigem Beispiel nennt man die Blätter des Binärbaumes. Diese zeichnen sich dadurch aus, dass ihre beiden Teilbäume leer sind, so dass von ihnen keine weiteren Teilbäume abzweigen. Die Knoten, die keine Blätter sind, nennt man auch innere Knoten.
Den Knoten kann man eine sogenannte Tiefe zuordnen. Dies kann man sich anschaulich so vorstellen, dass man der Wurzel des Binärbaumes die Tiefe 0 zuordnet und von da an zählt, wie viele Kanten man durchlaufen muss, bis man von der Wurzel aus den Knoten erreicht. Mit jeder Kante erhöht sich die Tiefe um 1.
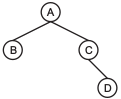
Zwei weitere Begriffe, die oft verwendet werden, sind die Begriffe Elternknoten und Kindknoten. In der kleinen Abbildung ist der Knoten A Elternknoten der beiden Knoten B und C. Umgekehrt sind B und C Kindknoten von A. Der Knoten B hat keine Kindknoten. Knoten C hat genau einen Kindknoten. Ein Knoten ohne Kindknoten ist, wie oben beschrieben, ein Blatt.
Die beschriebene Struktur kann durch eine solche Klasse modelliert werden:
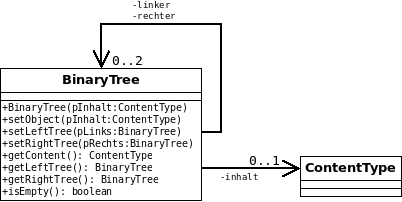
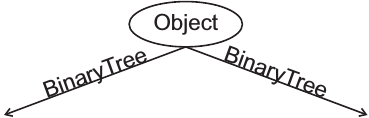
Diese Klasse ist mit sich selbst assoziiert. Dies ist uns schon von anderen Klassen, wie etwa Wartender oder Knoten vertraut.
Anders als diese kann ein Objekt der Klasse BinaryTree aber bis zu zwei Objekte derselben Klasse haben. Außerdem kann es ein Objekt der Klasse ContentType besitzen, das seinen Inhalt darstellt. Dies kann man sich noch einmal so veranschaulichen:
Kommen wir nun zu einer genaueren Beschreibung der Methoden, der Zentralabiturklasse NRW:
In dieser Klasse wurde sich dazu entschieden, dass ein leerer Binärbaum automatisch keine Teilbäume besitzt. Wenn ein Binärbaum aber ein Inhaltsobjekt (ungleich null) besitzt, dann besitzt er auch einen linken und rechten Teilbaum (die ggf. leer sein können).
Außerdem wird, wie gewohnt, eine generische Klasse verwendet. D.h., die Klasse ist genaugenommen BinaryTree<ContenType>, wie in den Beispielen weiter unten noch klar wird. Das Klassendiagramm der Abiturklasse wäre etwas anders als das Diagramm oben, weil dort noch eine private innere Klasse benutzt wird. Aber das ist für uns in der Anwendung zweitrangig.
| BinaryTree() | Ein leerer Binärbaum wird erzeugt. Seine Teilbäume sind null. |
| BinaryTree(ContentType pInhalt) | Ist pInhalt null, wird ein leerer Binärbaum erzeugt. Ist pInhalt nicht null, wird ein neuer Binärbaum erstellt, der pInhalt als Inhaltsobjekt besitzt. Seine beiden Teilbäume sind leer (aber nicht null). |
| BinaryTree(ContentType pInhalt,BinaryTree<ContentType> pLinker,BinaryTree<ContentType> pRechter) | Ist pInhalt nicht null, wird ein Binärbaum mit Inhalt pInhalt erstellt. Seine Teilbäume sind pLinker und pRechter. Ist einer der Parameter pLinker oder pRechter null, wird an entsprechender Stelle ein leerer Binärbaum eingesetzt. Ist pInhalt null, wird ein leerer Binärbaum erzeugt. |
| void setContent(ContentType pInhalt) | Ist der Binärbaum leer, wird ihm pInhalt als Inhaltsobjekt zugeordnet und zwei leere Teilbäume erzeugt. Ist er nicht leer, wird sein Inhaltsobjekt ersetzt und seine Teilbäume bleiben gleich. Ist jedoch pInhalt null, bleibt er unverändert. |
| void setLeftTree(BinaryTree<ContentType> pLinker) | Ist der Binärbaum nicht leer, wird ihm pLinker als linker Teilbaum zugeordnet. Ist jedoch der Binärbaum leer oder pLinker null, passiert nichts. |
| void setRightTree(BinaryTree<ContentType> pRechter) | Ist der Binärbaum nicht leer, wird ihm pRechter als rechter Teilbaum zugeordnet. Ist jedoch der Binärbaum leer oder pRechter null, passiert nichts. |
| ContentType getContent() | Liefert das Inhaltsobjekt des Binärbaumes. Falls er keines besitzt, wird null geliefert. |
| BinaryTree<ContentType> getLeftTree() | Liefert den linken Teilbaum des Binärbaumes. Falls kein linker Teilbaum existiert, wird null geliefert. |
| BinaryTree<ContentType> getRightTree() | Liefert den rechten Teilbaum des Binärbaumes. Falls kein rechter Teilbaum existiert, wird null geliefert. |
| boolean isEmpty() | Dies liefert den Wert true, wenn das Inhaltsobjekt des Binärbaumes null ist. Andernfalls wird der Wert false zurückgegeben. |
Anwendung
Speichern von Objekten
Um mit der Abiturklasse BinrayTree<ContentType> besser vertraut zu werden, verwenden wir im Folgenden diese Klasse – was sonst sollte man schon in einem Baum ablegen 😉
public class Apfel {
private boolean reif;
private double durchmesser;
public Apfel(boolean pReif, double pDurchmesser){
reif = pReif;
durchmesser = pDurchmesser;
}
public boolean getReif(){
return reif;
}
public double getDurchmesser(){
return durchmesser;
}
public void gibInfo(){
if (getReif())
System.out.print("Dieser Apfel ist reif");
else
System.out.print("Dieser Apfel ist nicht reif");
System.out.println(", sein Duchmesser ist "+getDurchmesser());
}
}
In diesem Beispiel sehen wir, wie man Objekte dieser Klasse in einem Binärbaum speichern kann. Als Übung ist es sinnvoll, sich einmal in einer Skizze klar zu machen, wie der Baum am Ende aussieht:
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree<Apfel> meinBaum = new BinaryTree<Apfel>(new Apfel(true, 6.5));
meinBaum.setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 5.0)));
meinBaum.setRightTree(new BinaryTree<Apfel>(null));
meinBaum.getRightTree().setContent(new Apfel(true, 5.5));
meinBaum.getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 5.0)));
meinBaum.getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(false, 5.0)));
meinBaum.getRightTree().getLeftTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 6.0)));
}
}
Umgekehrt kann man sich auch einen Baum vorgeben und versuchen, diesen zu konstruieren. Zum Beispiel diesen:
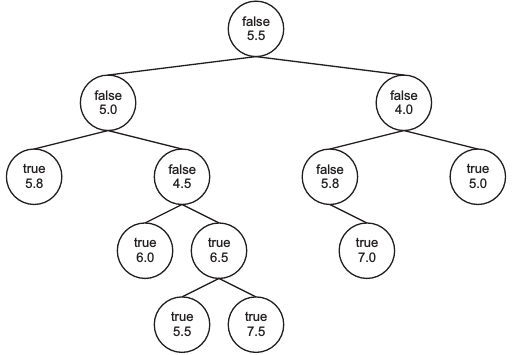
Eine mögliche Implementierung folgt nun – zur Übung solltest Du aber zuerst versuchen, diesen Baum zu erstellen ohne Dir die Lösung anzusehen 🙂
public class BinaryTreeBsp {
public static void main(String[] args) {
BinaryTree<Apfel> meinBaum = new BinaryTree<Apfel>(new Apfel(false, 5.5));
meinBaum.setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 5.0)));
meinBaum.setRightTree(new BinaryTree<Apfel>(new Apfel(false, 4.0)));
meinBaum.getLeftTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 5.8)));
meinBaum.getLeftTree().setRightTree(new BinaryTree<Apfel>(new Apfel(false, 4.5)));
meinBaum.getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 5.8)));
meinBaum.getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 5.0)));
meinBaum.getLeftTree().getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 6.0)));
meinBaum.getLeftTree().getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 6.5)));
meinBaum.getRightTree().getLeftTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 7.0)));
meinBaum.getLeftTree().getRightTree().getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 5.5)));
meinBaum.getLeftTree().getRightTree().getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 7.5)));
inorder(meinBaum);
}
}
Auslesen der gespeicherten Objekte
Möchte man die Daten, die in einem Binärbaum gespeichert sind, wieder ausgeben, ist zunächst nicht ganz klar, in welcher Reihenfolge man dies erledigen sollte. In der Tat gibt es verschiedene übliche Vorgehensweisen, um systematisch alle Knoten abzuarbeiten. Wir betrachten hier drei dieser Verfahren, die man auch Traversierungen oder Traversierungsalgorithmen nennt.
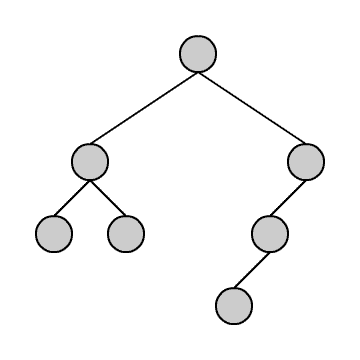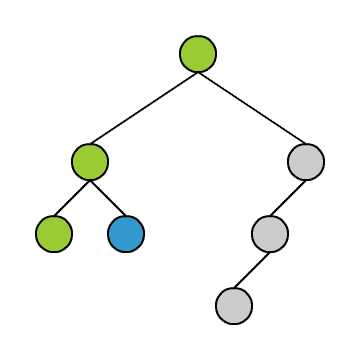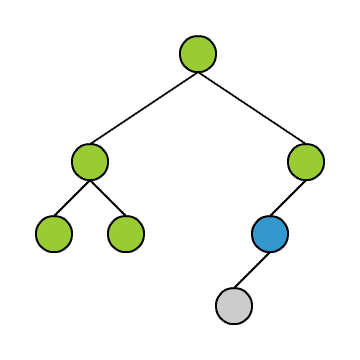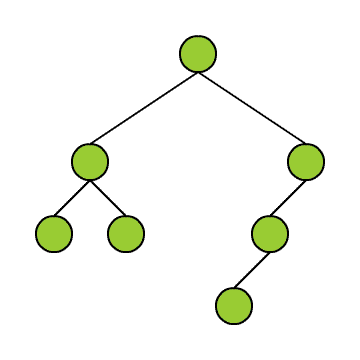
Alle drei Verfahren haben gemeinsam, dass man den Baum in derselben Weise durchläuft. Der Unterschied besteht darin, wann man das in einem Knoten vorgefundene Objekt ausgibt.
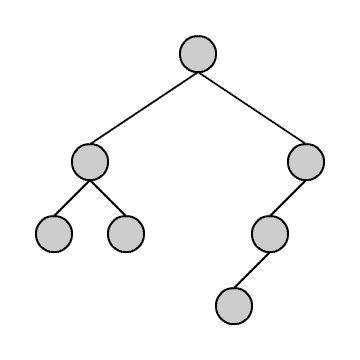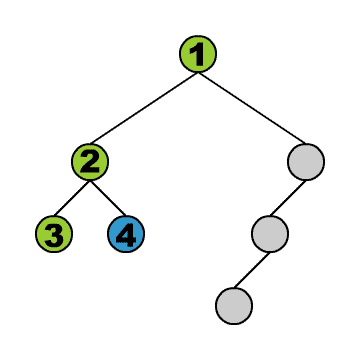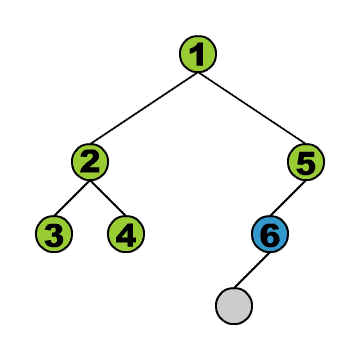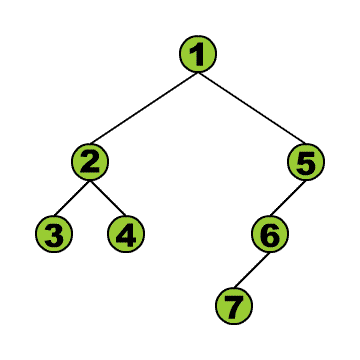
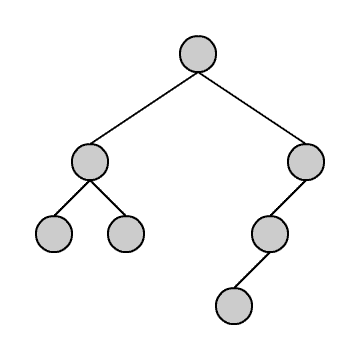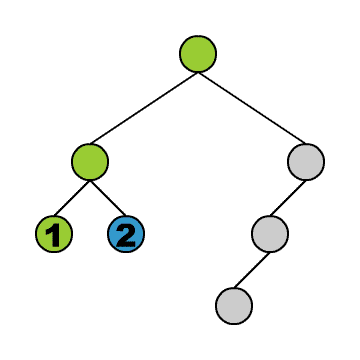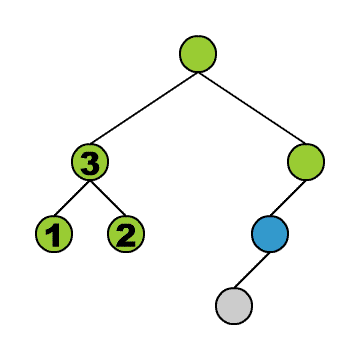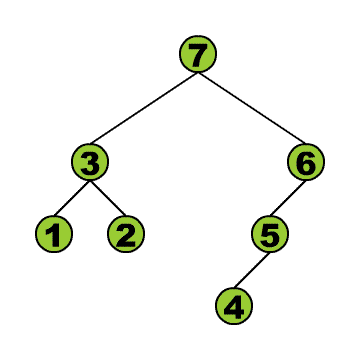
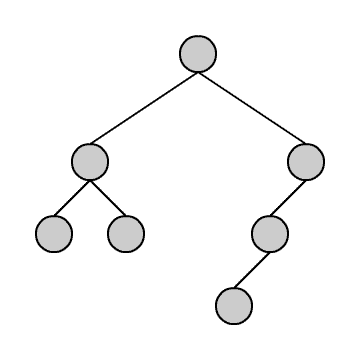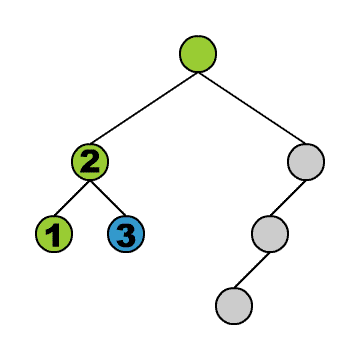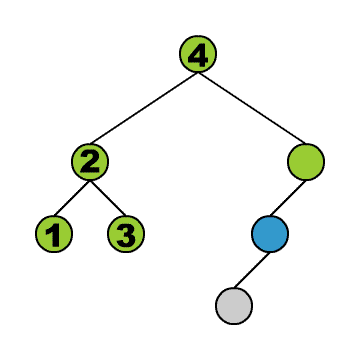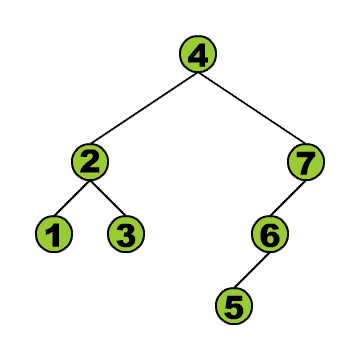
Das Durchlaufen können wir uns anhand der kleinen Animation verdeutlichen. Wir stellen uns vor, wir befinden uns immer in dem blauen Knoten. Die grünen Knoten sind die, die wir schon besucht haben.
Wir beginnen in der Wurzel und steigen dann solange wie möglich in den linken Teilbaum hinab. Geht es nicht weiter, gehen wir einen Schritt zurück und dann in den rechten Teilbaum. Von dort aus versuchen wir wieder zunächst möglichst weit links hinabzusteigen und so fort. Am Ende steigen wir wieder auf zur Wurzel.
Diesen Verfahren lässt sich übrigens sehr schön rekursiv beschreiben. (Rekursion wird bald an einer anderen Stelle auf meiner Seite noch genauer erklärt.)
Traversierung(Binärbaum b){
falls b einen linken Teilbaum l besitzt, starte Traversierung(l)
falls b einen rechten Teilbaum r besitzt, starte Traversierung(r)
}
Dies stellt nur das Ablaufen des Baums dar – eine Ausgabe geschieht nicht!
Nun stellt sich also die Frage, an welcher Stelle die Ausgabe der gepeicherten Objekte stattfinden soll.
Drei Arten der Traversierung
Wie oben beschrieben, wandern wir immer in derselben Weise durch einen Binärbaum. Dabei besuchen wir alle Knoten. Die inneren Knoten sogar mehrfach auf den Rückwegen von tiefer gelegenen Knoten.
Es gibt nun drei Möglichkeiten, wann wir das in einem Knoten gespeicherte Objekt betrachten bzw. uns anzeigen lassen. Diese nennt man Preorder, Postorder und Inorder:
- Preorder: Beim ersten Besuch eines Knotens wird sein Inhalt ausgelesen. Mit anderen Worten: Bevor seine Teilbäume betrachten werden. D.h., dass zum Beispiel der Inhalt der Wurzel als allererstes ausgelesen wird.
Sehen wir uns diese Traversierungen in einer Implementierung an:
public class BinaryTreeTest {
public static void main(String[] args) {
BinaryTree<Apfel> meinBaum = new BinaryTree<Apfel>(new Apfel(false, 5.5));
meinBaum.setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 5.0)));
meinBaum.setRightTree(new BinaryTree<Apfel>(new Apfel(false, 4.0)));
meinBaum.getLeftTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 5.8)));
meinBaum.getLeftTree().setRightTree(new BinaryTree<Apfel>(new Apfel(false, 4.5)));
meinBaum.getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(false, 5.8)));
meinBaum.getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 5.0)));
meinBaum.getLeftTree().getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 6.0)));
meinBaum.getLeftTree().getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 6.5)));
meinBaum.getRightTree().getLeftTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 7.0)));
meinBaum.getLeftTree().getRightTree().getRightTree().setLeftTree(new BinaryTree<Apfel>(new Apfel(true, 5.5)));
meinBaum.getLeftTree().getRightTree().getRightTree().setRightTree(new BinaryTree<Apfel>(new Apfel(true, 7.5)));
preorder(meinBaum);
postorder(meinBaum);
inorder(meinBaum);
}
private static void preorder(BinaryTree<Apfel> pBaum){
if (!pBaum.isEmpty())
pBaum.getContent().gibInfo();
if (pBaum.getLeftTree() != null)
preorder(pBaum.getLeftTree());
if (pBaum.getRightTree() != null)
preorder(pBaum.getRightTree());
}
private static void inorder(BinaryTree<Apfel> pBaum){
if (pBaum.getLeftTree() != null)
inorder(pBaum.getLeftTree());
if (!pBaum.isEmpty())
pBaum.getContent().gibInfo();
if (pBaum.getRightTree() != null)
inorder(pBaum.getRightTree());
}
private static void postorder(BinaryTree<Apfel> pBaum){
if (pBaum.getLeftTree() != null)
postorder(pBaum.getLeftTree());
if (pBaum.getRightTree() != null)
postorder(pBaum.getRightTree());
if (!pBaum.isEmpty())
pBaum.getContent().gibInfo();
}
}
Startest Du dieses Beispiel, kannst Du gut versuchen, nachzuvollziehen, wie der Baum abgearbeitet wird.
In den Implementierungen der drei Methoden zur Traversierung sieht man übrigens nochmal schön, wie ähnlich sie sich letztlich sind – einzig die Position der Ausgabe unterscheidet sich.
Sortieren mit Binärbäumen
Binärbäume erweisen sich als sehr nützlich, wenn es darum geht, Objekte nach einem bestimmten Kriterium zu sortieren. Wie dies genau gemeint ist, betrachten wir wieder am Beispiel der Klasse Apfel.

Nehmen wir an, wir haben einen Korb reifer Äpfel vor uns liegen. Diese sollen nun dem Durchmesser nach (in aufsteigender Reihenfolge) sortiert werden. Wir ziehen den ersten Apfel aus dem Korb, stellen fest, dass er einen Durchmesser von 6.5 cm hat und fügen ihn in einen neuen Binärbaum ein:
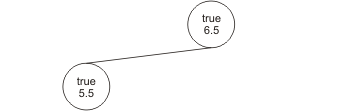
Nun ziehen wir den zweiten Apfel aus dem Korb. Dieser hat einen Durchmesser von 5.5 cm. Da er also einen kleineren Durchmesser hat, fügen wir ihn als linken Kindknoten an die Wurzel unseres Binärbaumes an:
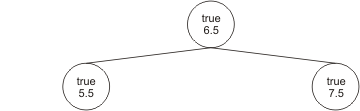
Der dritte Apfel, den wir ziehen, hat einen Durchmesser von 7.5 cm. Da dieser größer ist als der Apfel, der die Wurzel des Baumes bildet, wird er als rechter Kindknoten der Wurzel hinzugefügt:
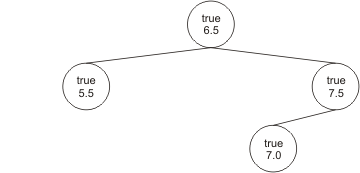
Nun wird es etwas interessanter. Der vierte Apfel hat einen Durchmesser von 7.0 cm}. Da er damit größer ist als der in der Wurzel, suchen wir im rechten Teilbaum nach einer geeigneten Position. Der Apfel in der Wurzel des rechten Teilbaumes (also der mit Durchmesser 7.5 cm) ist größer als der neue Apfel. Daher muss der neue Apfel als linker Kindknoten von diesem hinzugefügt werden:
An diesen Beispielen erkennt man schon das Muster, nach dem sortiert wird: Man vergleicht den neuen Apfel zunächst mit dem in der Wurzel, entscheidet dann, ob man im linken oder rechten Teilbaum weiter nach der richtigen Position suchen muss und setzt dort seine Suche auf dieselbe Weise fort. Hier steckt also wieder eine Rekursion hinter!
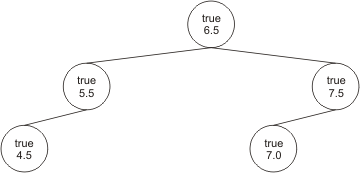
Der fünfte Apfel hat einen Durchmesser von 4.5 cm. Wir vergleichen ihn also zuerst mit dem in der Wurzel, sehen, dass wir in den linken Teilbaum wechseln müssen, vergleichen dort mit der Wurzel und stellen fest, dass er als linker Kindknoten hinzugefügt werden muss:
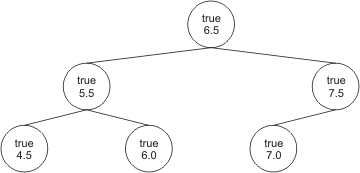
Zuletzt haben wir noch einen Apfel mit Durchmesser 6.0 cm, der entsprechend so einsortiert wird:
Übrigens: Es kann sich mit denselben Äpfeln auch eine anderen sortierter Binärbaum ergeben! Hätten wir als erstes z.B. den Apfel mit 4.5 cm Durchmesser erwischt und einsortiert, läge nun dieser oben in der Wurzel.
Wenn man einen in dieser Weise sortieren Baum betrachten, sollte man erkennen, dass bei einer Inorder-Traversierung die Objekte (also in diesem Fall die Äpfel) in aufsteigender Reihenfolge ausgegeben werden.
Nun besteht eine Herausforderung natürlich noch darin, das hier beschriebene Sortierverfahren zu implementieren! Eine Lösung will ich hier nicht vorwegnehmen, sondern nur den Tipp geben, dass dieses Verfahren Rekursion verwenden sollte!