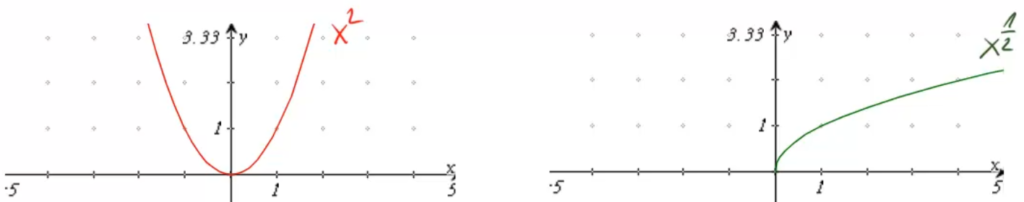- Potenzfunktionen mit natürlichem Exponenten
- Einführung
- Potenzfunktionen mit geradem Exponenten
- Potenzfunktionen mit ungeradem Exponenten
- Vertiefung zur Symmetrie
- Vertiefung zum Globalverhalten
- Die Wachstumseigenschaft
- Potenzielles Wachstum
- Potenzfunktionen mit negativen ganzzahligen Exponenten
- Einführung
- Besonderheiten der Graphen
- Potenzfunktionen mit Brüchen im Exponenten
- Einführung
- Wertetabelle und Graph
Potenzfunktionen mit natürlichem Exponenten
Einführung
Wiedergabe stellt eine Verbindung zu YouTube her.
In der Mittelstufe haben wir die Funktion ![]() bereits kennengelernt. Diese sehr einfache quadratische Funktion beschreibt die Normalparabel.
bereits kennengelernt. Diese sehr einfache quadratische Funktion beschreibt die Normalparabel.
Wir sehen uns nun Funktionen an, deren Term sehr ähnlich aussieht: Statt der ![]() im Exponenten setzen wir nun verschiedene natürliche Zahlen ein, d.h., wir betrachten Funktionen der Form
im Exponenten setzen wir nun verschiedene natürliche Zahlen ein, d.h., wir betrachten Funktionen der Form
![]()
wobei
Potenzfunktionen mit geradem Exponenten
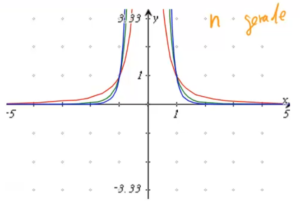
Sehen wir uns als Beispiele für Funktionen mit geradem Exponenten die Graphen der Funktionen ![]() ,
, ![]() und
und ![]() an:
an:
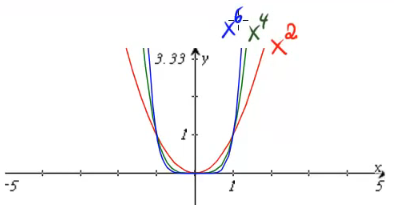
In Rot sehen wir wieder die bekannte Normalprabel. Die anderen beiden Graphen besitzen zwar eine gewisse Ähnlichkeit dazu, aber sie verlaufen im Bereich um den Ursprung deutlich flacher, werden dann jedoch steiler. Trotz der Ähnlichkeit zu einer Parabel werden diese Kurven aber nicht als Parabeln bezeichnet.
Halten wir einige Gemeinsamkeiten der Graphen fest:
- Alle Graphen verlaufen durch den Ursprung
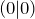 .
. - Alle Graphen sind achsensymmetrisch bezüglich der
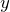 -Achse, d.h., die werden an dieser Achse gespiegelt.
-Achse, d.h., die werden an dieser Achse gespiegelt. - Die Graphen kommen nie in den Bereich unterhalb der
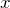 -Achse.
-Achse. - Alle Graphen verlaufen durch die beiden Punkte
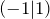 und
und 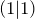 .
. - Geht man immer weiter nach rechts oder immer weiter nach links, so steigen die Graphen immer weiter nach oben bis „ins Unendliche“.
Potenzfunktionen mit ungeradem Exponenten
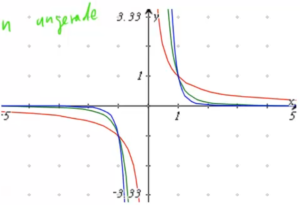
Kommen wir nun zu Beispielen mit ungeraden Exponenten. Hier betrachten wir exemplarisch die Exponenten ![]() ,
, ![]() und
und ![]() :
:
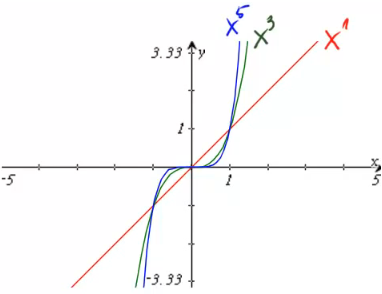
Der Graph zu ![]() fällt etwas aus der Reihe, da er als einziger eine Gerade beschreibt. Dennoch gelten alle folgenden Gemeinsamkeiten auch für ihn:
fällt etwas aus der Reihe, da er als einziger eine Gerade beschreibt. Dennoch gelten alle folgenden Gemeinsamkeiten auch für ihn:
- Alle Graphen verlaufen durch den Ursprung
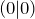 .
. - Alle Graphen sind punktsymmetrisch bezüglich des Ursprungs.
- Alle Graphen verlaufen durch die beiden Punkte
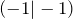 und
und 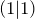 .
. - Geht man immer weiter nach rechts, so steigen die Graphen immer weiter nach oben bis „ins Unendliche“.
- Geht man immer weiter nach links, so fallen die Graphen immer weiter nach unten bis „ins negative Unendliche“.
Vertiefung zur Symmetrie
Die beiden beobachteten Symmetrien können wir auch mathematisch wie folgt beschreiben:
| Der Graph einer Funktion | Der Graph einer Funktion |
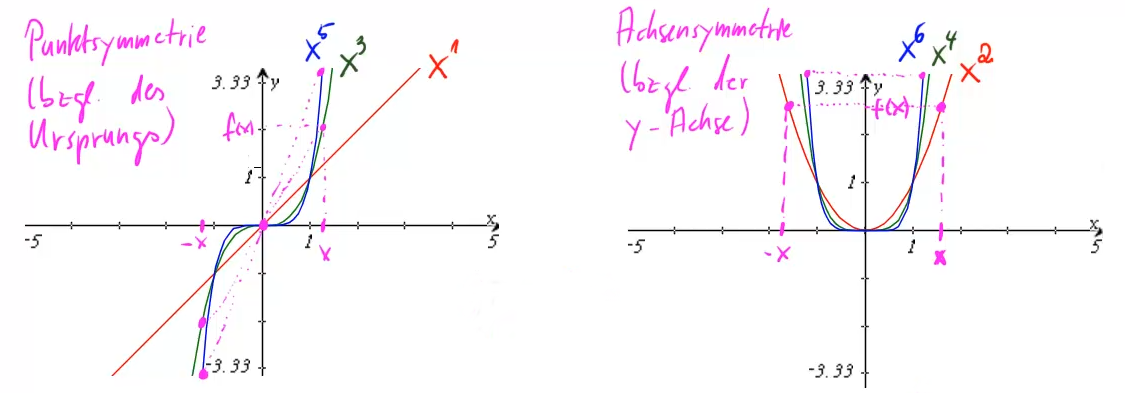
Betrachten wir als Beispiel ![]() . Hier gilt beispielsweise
. Hier gilt beispielsweise ![]() . D.h., wenn wir vom Ursprung aus
. D.h., wenn wir vom Ursprung aus ![]() Einheiten nach rechts gehen, dann müssen wir
Einheiten nach rechts gehen, dann müssen wir ![]() Einheiten nach oben, um auf dem Graphen zu bleiben. Gehen wir hingegen vom Ursprung aus
Einheiten nach oben, um auf dem Graphen zu bleiben. Gehen wir hingegen vom Ursprung aus ![]() Einheiten nach links, so müssen wir
Einheiten nach links, so müssen wir ![]() Einheiten nach unten – also genau in die andere Richtung. Es gilt also
Einheiten nach unten – also genau in die andere Richtung. Es gilt also ![]() .
.
Betrachten wir hingegen ![]() , ergibt sich ein anderes Bild. Hier gilt
, ergibt sich ein anderes Bild. Hier gilt ![]() und ebenfalls
und ebenfalls ![]() . D.h., wenn wir vom Ursprung aus
. D.h., wenn wir vom Ursprung aus ![]() Einheiten nach rechts oder links gehen, müssen wir in beiden Fällen
Einheiten nach rechts oder links gehen, müssen wir in beiden Fällen ![]() Einheiten nach oben, um auf dem Graphen zu bleiben.
Einheiten nach oben, um auf dem Graphen zu bleiben.
Dieser Unterschied ergibt sich daraus, dass bei den geraden Exponenten das negative Vorzeichen verloren geht. Bei einem ungeraden Exponenten hingegen bleibt das Vorzeichen erhalten.
Vertiefung zum Globalverhalten
Mit dem Globalverhalten beschreibt man, was geschieht, wenn man in eine Funktion immer größere ![]() -Werte oder auch immer kleinere negative
-Werte oder auch immer kleinere negative ![]() -Werte einsetzt. Mit anderen Worten: Man untersucht, wie sich der Graph verhält, wenn man auf der
-Werte einsetzt. Mit anderen Worten: Man untersucht, wie sich der Graph verhält, wenn man auf der ![]() -Achse immer weiter nach rechts oder immer weiter nach links wandert.
-Achse immer weiter nach rechts oder immer weiter nach links wandert.
Etwas formaler sagt man, man betrachtet, was passiert, wenn ![]() gegen unendlich geht (in Zeichen
gegen unendlich geht (in Zeichen ![]() ) oder gegen minus unendlich geht (in Zeichen
) oder gegen minus unendlich geht (in Zeichen ![]() ).
).
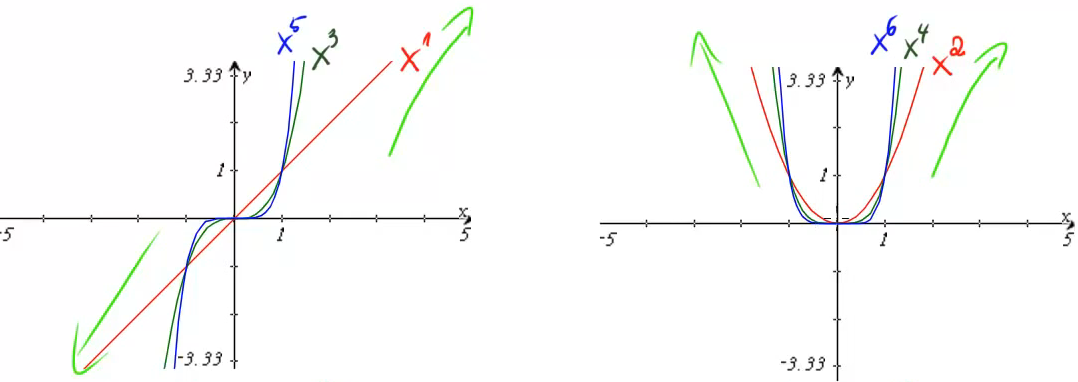
Wir haben bereits gesehen, dass das Globalverhalten bei Potenzefunktionen davon abhängt, ob der Exponent gerade oder ungerade ist:
| Ungerader Exponent | Gerader Exponent | |
| Der Graph wandert unendlich weit nach oben, d.h., | Der Graph wandert unendlich weit nach oben, d.h., | |
| Der Graph wandert unendlich weit nach unten, d.h., | Der Graph wandert unendlich weit nach oben, d.h., |
Die Wachstumseigenschaft
Wiedergabe stellt eine Verbindung zu YouTube her.
Bei der Wachstumseigenschaft fragt man sich, ob es Regelmäßigkeiten beim Zusammenhang zwischen den ![]() – und
– und ![]() -Werten gibt, oder anders ausgedrückt, ob es Veränderungen des
-Werten gibt, oder anders ausgedrückt, ob es Veränderungen des ![]() -Wertes bei denen man besonders schön die Veränderung des
-Wertes bei denen man besonders schön die Veränderung des ![]() -Wertes beschreiben kann.
-Wertes beschreiben kann.
Sehen wir uns dazu ein paar Beispielfunktionen an:
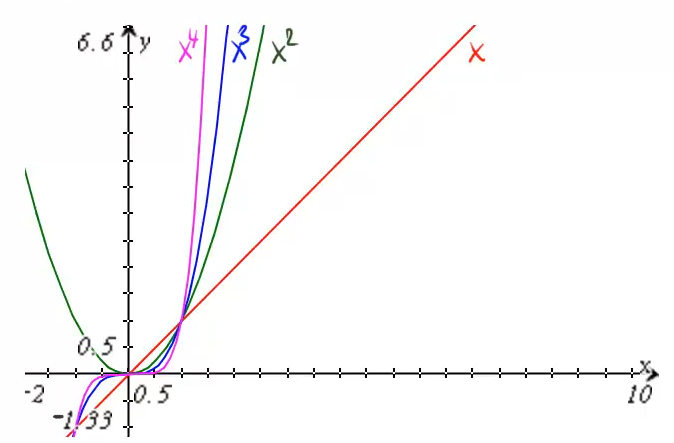
Die Funktion ![]() (deren Graph hier in Rot zu sehen ist) ist natürlich besonders einfach. Eine Veränderung des
(deren Graph hier in Rot zu sehen ist) ist natürlich besonders einfach. Eine Veränderung des ![]() -Wertes überträgt sich unmittelbar auf den
-Wertes überträgt sich unmittelbar auf den ![]() -Wert.
-Wert.
Wird z.B. der ![]() -Wert
-Wert ![]() größer, dann auch der
größer, dann auch der ![]() -Wert. Wird der
-Wert. Wird der ![]() -Wert verdoppelt, so verdoppelt sich auch der
-Wert verdoppelt, so verdoppelt sich auch der ![]() -Wert.
-Wert.
Wie sieht es bei der Funktion ![]() (mit dem blauen Graphen) aus?
(mit dem blauen Graphen) aus?
Wenn wir hier auf den ![]() -Wert einen festen Wert addieren, ist beim
-Wert einen festen Wert addieren, ist beim ![]() -Wert beine klare Regelmäßigkeit zu erkennen:
-Wert beine klare Regelmäßigkeit zu erkennen:
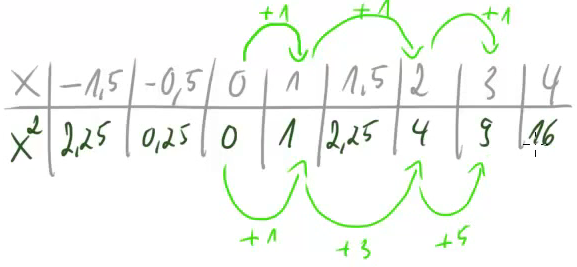
Der Ansatz, immer einen festen Wert zu addieren, ist hier also nicht zielführend.
Anders sieht es aber aus, wenn wir den ![]() -Wert immer mit einer festen Zahl multiplizieren. Beispielsweise könnten wir ihn immer verdoppeln:
-Wert immer mit einer festen Zahl multiplizieren. Beispielsweise könnten wir ihn immer verdoppeln:
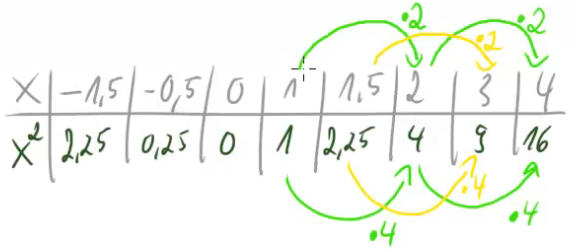
Wir sehen, dass sich der ![]() -Wert immer vervierfacht, wenn wir den
-Wert immer vervierfacht, wenn wir den ![]() -Wert vedoppeln.
-Wert vedoppeln.
Nun stellt sich die Frage, was passiert, wenn wir mit anderen Zahlen multiplizieren:
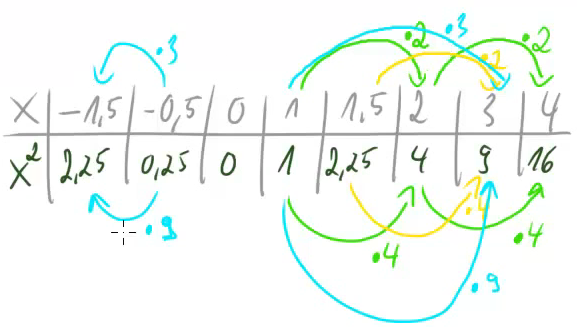
Halten wir einmal in einer Tabelle fest, welche Regeln man hier erkennen oder auch allgemein vermuten kann:
Die allgemeine Regel in der letzten Zeile kann man auch schreiben als ![]() .
.
Auch bei den anderen Potenzfunktionen können wir eine solche Regel finden. Für eine belieibige Potenzfunktion ![]() gilt:
gilt:
![]()
Dass diese sogenannte Wachstumseigenschaft tatsächlich gilt, sehen wir mit einer kleinen Rechnung:
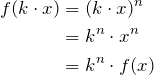
Potenzielles Wachstum
Wiedergabe stellt eine Verbindung zu YouTube her.
Wenn wir statt nur Funktionen der Form ![]() etwas allgemeiner auch die Form
etwas allgemeiner auch die Form
![]()
mit einer festen Zahl
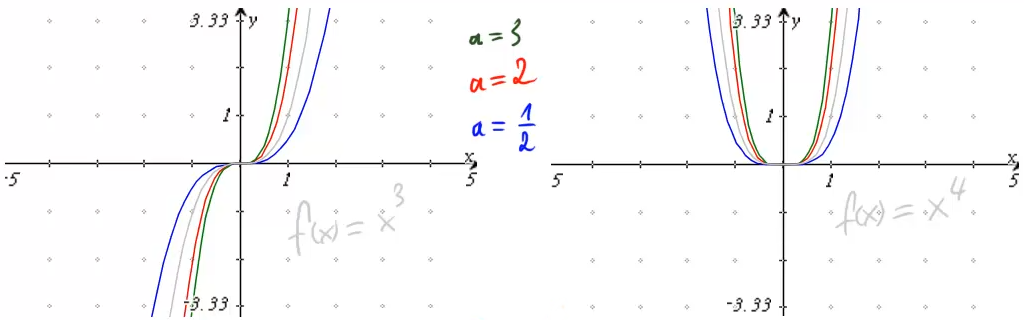
Ist ![]() positiv, dann ergeben sich die zugehörigen Graphen aus den uns schon bekannten Graphen durch Strecken oder Stauchen:
positiv, dann ergeben sich die zugehörigen Graphen aus den uns schon bekannten Graphen durch Strecken oder Stauchen:
Ist ![]() hingegen negativ, dann wird der Graph zusätzlich an der
hingegen negativ, dann wird der Graph zusätzlich an der ![]() -Achse gespiegelt:
-Achse gespiegelt:
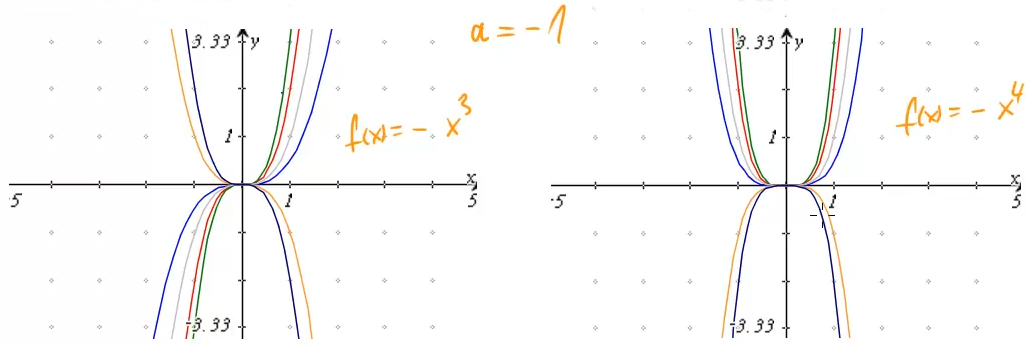
Wie der sogenannte Streckungsfaktor ![]() lautet, lässt sich gut am Graphen erkennen: Man muss nur den
lautet, lässt sich gut am Graphen erkennen: Man muss nur den ![]() -Wert bei
-Wert bei ![]() ablesen.
ablesen.
Das liegt daran, dass ![]() gilt.
gilt.
Die Wachstumseigenschaft bleibt übrigens auch hier richtig, d.h., auch hier gilt ![]() .
.
Wiedergabe stellt eine Verbindung zu YouTube her.
Potenzfunktionen mit negativen ganzzahligen Exponenten
Wiedergabe stellt eine Verbindung zu YouTube her.
Einführung
Sehen wir uns zur Einführung dieser Art von Funktion ein paar dazu passende Sachzusammenhänge an.
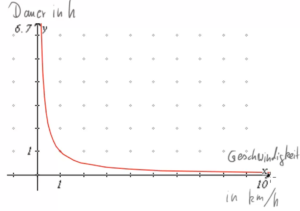
Stellen wir uns als Erstes vor, wir hätten jeden Morgen einen Schulweg von einem Kilometer zurückzulegen. Natürlich sind wir nicht jeden Tag gleich schnell unterwegs. Je schneller wir gehen, desto kürzer ist die Dauer des Wegs.
Gehen wir zum Beispiel mit einer (sehr langsamen) Geschwindigkeit von ![]() , so brauchen wir genau eine Stunde – denn pro Stunde schaffen wir dann ja genau einen Kilometer.
, so brauchen wir genau eine Stunde – denn pro Stunde schaffen wir dann ja genau einen Kilometer.
Sind aber aber zügiger unterwegs und gehen mit ![]() , so brauchen wir für den einen Kilometer nur
, so brauchen wir für den einen Kilometer nur ![]() Stunde – denn pro Stunde würden wir ja sechs Kilometer hinter uns legen – oder mit anderen Worten, 10 Minuten.
Stunde – denn pro Stunde würden wir ja sechs Kilometer hinter uns legen – oder mit anderen Worten, 10 Minuten.
Wie lange wir bei einer bestimmten Geschwindigkeit benötigen, können wir einfach ausrechnen, indem wir den gegeben einen Kilometer durch die Geschwindigkeit teilen:
![]()
Wenn wir die Geschwindigkeit in km/h mit ![]() bezeichnen, dann gibt uns also die Funktion
bezeichnen, dann gibt uns also die Funktion ![]() die Dauer in Stunden an.
die Dauer in Stunden an.
Was aber hat dies mit negativen Exponenten zu tun? Das sehen wir, wenn wir uns daran erinnern, dass man laut der Potenzgesetze ![]() auch als
auch als ![]() schreiben kann. Unsere Funktion lautet damit
schreiben kann. Unsere Funktion lautet damit ![]() , womit wir das erste Beispiel für eine Potenzfunktion mit einem negativen Exponenten haben!
, womit wir das erste Beispiel für eine Potenzfunktion mit einem negativen Exponenten haben!
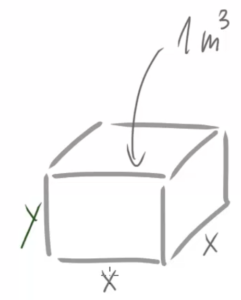
Kommen wir zu einem zweiten Beispiel. Hier stellen wir uns vor, wir sollen einen quaderförmigen Kasten konstruieren, der ein Volumen von genau ![]() hat. Die Grundfläche ist quadratisch mit Seitenlängen
hat. Die Grundfläche ist quadratisch mit Seitenlängen ![]() , d.h., er ist
, d.h., er ist ![]() breit und lang. Die passende Höhe
breit und lang. Die passende Höhe ![]() soll in Abhängigkeit von
soll in Abhängigkeit von ![]() bestimmt werden.
bestimmt werden.
Ist ![]() zum Beispiel
zum Beispiel ![]() , dann muss
, dann muss ![]() ebenfalls
ebenfalls ![]() lang sein, denn dann beträgt sein Volumen
lang sein, denn dann beträgt sein Volumen ![]() , denn um das Volumen zu berechnen, muss man alle drei Seitenlängen multiplizieren.
, denn um das Volumen zu berechnen, muss man alle drei Seitenlängen multiplizieren.
Wie hoch muss der Kasten aber sein, wenn ![]() stattdessen
stattdessen ![]() lang ist?
lang ist?
In diesem Fall beträgt sein Volumen ![]() . Damit dies
. Damit dies ![]() ergibt, muss also
ergibt, muss also ![]() sein.
sein.
Allgemein muss gelten ![]() oder kurz
oder kurz ![]() . Lösen wir dies nach
. Lösen wir dies nach ![]() auf, erhalten wir
auf, erhalten wir
![]()
Der Graph dieser Funktion sieht dem Graphen aus dem ersten Beispiel recht ähnlich. Im Detail unterscheiden sie sich jedoch. Dies betrachten wir nun etwas genauer.
Sieht man genau hin, erkennt man, dass er nahe der ![]() -Achse steiler ist und sich für wachsende
-Achse steiler ist und sich für wachsende ![]() -Werte schneller der
-Werte schneller der ![]() -Achse annähert.
-Achse annähert.
Besonderheiten der Graphen
Wir betrachten die Graphen der Funktionen ab nun auch für negative ![]() -Werte, da so einige Unterschiede erst sichtbar werden.
-Werte, da so einige Unterschiede erst sichtbar werden.
Hier sehen wir ein paar Graphen zu Funktionen mit negativen geradem Exponenten, also zum Beispiel ![]() .
.
Folgende Besonderheiten fallen auf:
- Die Graphen sind achsensymmetrisch bezüglich der
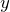 -Achse.
-Achse. - Sie verlaufen alle durch die Punkte
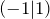 und
und 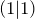 .
. - Nahe der
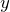 -Achse steigen sie ins Unendliche.
-Achse steigen sie ins Unendliche. - Es gibt nur positive Funktionswerte.
- Jede postive Zahl kommt als
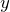 -Wert vor.
-Wert vor. - Für
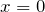 gibt es keinen
gibt es keinen 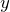 -Wert.
-Wert. - Die Graphen schneiden nie die
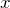 -Achse.
-Achse. - Für wachsende
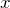 -Werte nähern sie sich asymptotisch der
-Werte nähern sie sich asymptotisch der 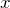 -Achse an, für sinkende negative
-Achse an, für sinkende negative 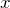 -Werte ebenfalls.
-Werte ebenfalls.
Ein Verhalten wie bei diesen Graphen bei ![]() haben wir bisher noch nicht gesehen. Man sagt, dass dort ein Pol ohne Vorzeichenwechsel vorliegt.
haben wir bisher noch nicht gesehen. Man sagt, dass dort ein Pol ohne Vorzeichenwechsel vorliegt.
Dass es für ![]() keinen
keinen ![]() -Wert gibt, liegt daran, dass man in diese Funktionen
-Wert gibt, liegt daran, dass man in diese Funktionen ![]() nicht einsetzen darf, denn dann würde man durch Null teilen! Man spricht hier auch von einer Definitionslücke. Das soll heißen, dass der Funktionswert für
nicht einsetzen darf, denn dann würde man durch Null teilen! Man spricht hier auch von einer Definitionslücke. Das soll heißen, dass der Funktionswert für ![]() nicht definiert ist.
nicht definiert ist.
Kommen wir nun zu Funktionen mit ungeradem Exponent.
Folgende Besonderheiten fallen hier auf:
- Die Graphen sind punktsymmetrisch bezüglich des Ursprungs.
- Sie verlaufen alle durch die Punkte
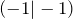 und
und 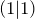 .
. - Es gibt postive und negative
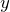 -Werte.
-Werte. - Jede Zahl außer Null kommt als
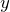 -Wert vor.
-Wert vor. - Nahe der
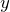 -Achse wandern sie rechts ins Unendliche, links jedoch fallen sie ins negative Unendliche.
-Achse wandern sie rechts ins Unendliche, links jedoch fallen sie ins negative Unendliche. - Für
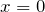 gibt es keinen
gibt es keinen 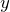 -Wert.
-Wert. - Die Graphen schneiden nie die
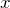 -Achse.
-Achse. - Für wachsende
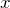 -Werte nähern sie sich von oben asymptotisch der
-Werte nähern sie sich von oben asymptotisch der 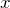 -Achse an, für sinkende negative
-Achse an, für sinkende negative 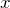 -Werte nähern sie sich von unten an diese.
-Werte nähern sie sich von unten an diese.
Bei diesen Graphen spricht man bei ![]() von einem Pol mit Vorzeichenwechsel.
von einem Pol mit Vorzeichenwechsel.
Wiedergabe stellt eine Verbindung zu YouTube her.
Potenzfunktionen mit Brüchen im Exponenten
Wiedergabe stellt eine Verbindung zu YouTube her.
Einführung
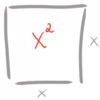
Betrachten wir hier zunächst eine Situation, die uns bekannt vorkommen sollte.
Angenommen, wir haben ein Quadrat mit der Seitenlänge ![]() vorliegen. Dann beträgt sein Flächeninhalt
vorliegen. Dann beträgt sein Flächeninhalt ![]() .
.
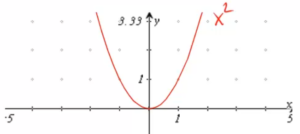
Stellen wir den Flächeninhalt in Abhängigkeit der Seitenlänge ![]() dar, erhalten wir die uns bekannt Funktion
dar, erhalten wir die uns bekannt Funktion ![]() . Der Graph dieser Funktion ist die Normalparabel.
. Der Graph dieser Funktion ist die Normalparabel.
Nun betrachten wir die umgekehrte Situation.
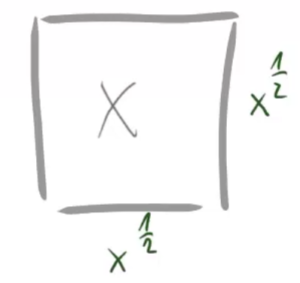
In einem anderen Quadrat geben wir vor, dass der Flächeninhalt ![]() betragen soll. Die Frage ist nun, wie die Seitenlänge gewählt werden muss, damit das Quadrat diesen gewünschten Flächeninhalt hat.
betragen soll. Die Frage ist nun, wie die Seitenlänge gewählt werden muss, damit das Quadrat diesen gewünschten Flächeninhalt hat.
Geben wir zum Beispiel den Flächeninhalt ![]() vor, dann müssen wir die Seitenlänge
vor, dann müssen wir die Seitenlänge ![]() wählen, denn
wählen, denn ![]() .
.
Allgemein muss die Seitenlänge also so gewählt werden, dass sie mit sich selbst multipliziert den Flächeninhalt ![]() ergibt. Mit anderen Worten, ihr Quadrat muss
ergibt. Mit anderen Worten, ihr Quadrat muss ![]() ergeben.
ergeben.
Daran erkennen wir, dass die Seitenlänge genau die Wurzel von ![]() sein muss. In dieser Situation erhalten wir also die Funktion
sein muss. In dieser Situation erhalten wir also die Funktion ![]() . Die Potenzgesetze sagen uns, dass wir dies aber auch schreiben können als
. Die Potenzgesetze sagen uns, dass wir dies aber auch schreiben können als ![]() . So haben wir das erste Beispiel für eine Potenzfunktion mit einem Bruch im Exponenten gefunden.
. So haben wir das erste Beispiel für eine Potenzfunktion mit einem Bruch im Exponenten gefunden.
Wertetabelle und Graph
Vergleichen wir einmal die Wertetabellen der beiden oben beschriebenen Funktionen:
Diese beiden Wertetabellen sehen fast gleich aus. Lediglich die beiden Zeilen wurden vertauscht, was im Kontext ja durchaus auch logisch erscheint.
Diesen Vertauschen den beiden Zeilen, wird auch deutlich, wenn wir die Graphen der beiden Funktionen betrachten:
Auf den ersten Blick könnte man meinen, die halbe Normalparabel muss gedreht werden, um den rechten Graphen zu erhalten. Das stimmt so aber nicht. In Wahrheit wird der rechte Teil der Normalparabel an der sogenannten Winkelhalbierenden gespiegelt. Das ist die Ursprungsgerade mit Steigung 1.
Für die Erstellung der Inhalte wurde die Software des TI-Nspire™ CX CAS verwendet, eingetragene Warenzeichen von Texas Instruments.