Wiedergabe stellt eine Verbindung zu YouTube her.
Einem Rechner müssen wir – dank dieser Beobachtungen zur Subtraktion – die Subtraktion nicht komplett neu beibringen. Im Grunde müssen wir nur eine Schaltung konstruieren, mit der wir die Gegenzahl einer Binärzahl bilden können. Wenn wir das geschafft haben, können wir wieder auf die Addition zurückgreifen. Zur Erinnerung:
| Bestimmen der Gegenzahl: Invertiere in der Dualzahl alle Ziffern, d.h., aus 1 mache 0 und umgekehrt. Anschließend addiere 1 darauf. Sollte das Ergebnis mehr Stellen haben, als im Computer verwendet werden, so streiche die vorderste Stelle einfach weg. |
Die Konstruktion einer Schaltung zur Bildung der Gegenzahl ist etwas kniffelig:
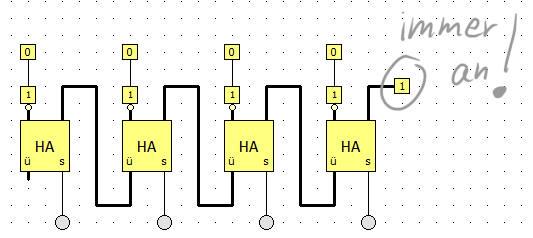
Mit den oberen vier Schaltern kann man eine vierstellige Dualzahl eingeben. Der Schalter ganz rechts muss immer eingeschaltet sein.
Wir sollten einmal genau nachvollziehen, wieso diese Schaltung tatsächlich die Gegenzahl bilden kann. Wie wir sehen, werden die vier Ziffern, die an den Schaltern angegebenen werden, zuerst in Inverter geleitet. Dies entspricht genau dem Umkehren der Ziffern. Der Schalter ganz rechts symbolisiert die 1, die danach addiert werden muss. Diese Addition findet findet dann in den vier Halbaddierern statt.
Wiedergabe stellt eine Verbindung zu YouTube her.
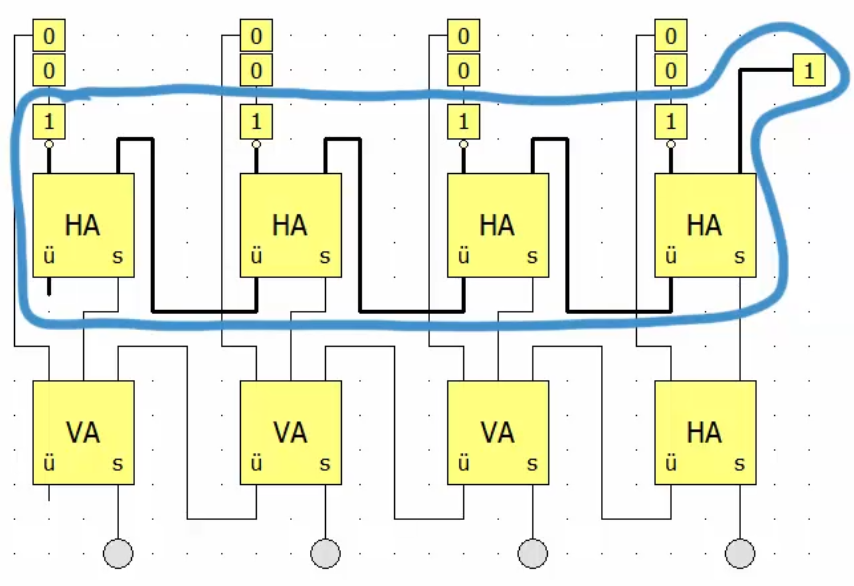
Nun können wir diese Schaltung zu einem 4-Bit-Subtrahierer erweitern. Dazu erinnern wir uns nochmal daran, dass die Gegenzahl von der Zahl die abgezogen wird gebildet wird. Die andere Zahl bleibt unverändert. Danach werden die unveränderte Zahl und die Gegenzahl addiert: