Die Gegenzahl einer Binärzahl
Wiedergabe stellt eine Verbindung zu YouTube her.
Wir stellen uns wieder vor, dass wir einen Computer verwenden, der mit vier Stellen rechnet:
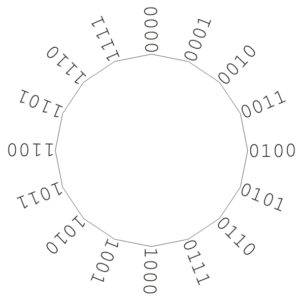
Wie wir schon gesehen haben, kann man Additionen veranschaulichen, indem man in diesem Kreis im Uhrzeigersinn wandert. Allerdings gab es da Probleme, wenn das Ergebnis zu groß ist. Addieren wir zum Beispiel zu 1011(2) die 0111(2), so überschreiten wir die 0000(2) und landen bei der 0010(2), obwohl das richtige Ergebnis eigentlich 10010(2) wäre. Das Schöne ist aber, dass man sich diesen vermeintlichen Mangel für die Darstellung der Subtraktion zunutze macht!
Schauen wir uns nochmal das Zahlenbeispiel an. Wir sind bei der 1011(2) gestartet und bei der 0010(2) gelandet. Dasselbe hätten wir auch erreicht, wenn wir anstatt 7(10) = 0111(2) im Uhrzeigersinn 9(10) = 1001(2)gegen den Uhrzeigersinn gegangen wären.
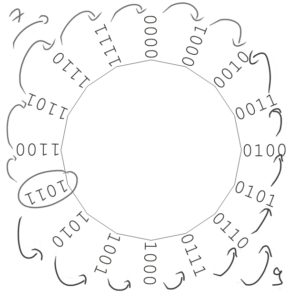
Was hat das mit einer Subtraktion zu tun? Ganz einfach: 1011(2) – 1001(2) = 0010(2). Wir haben hier also 9 subtrahiert.
Noch ein Beispiel. Wir starten erneut bei der 1011(2) und wollen 0100(2) = 4(10) subtrahieren. Wir haben die Wahl: Entweder wir wandern 4 gegen den Uhrzeigersinn oder 12 im Uhrzeigersinn, um beim Ergebnis 0111(2) zu landen.
Durch unsere Beobachtungen können wir nun eine Subtraktion in eine Addition umwandeln – oder anschaulich gesprochen ein Wandern gegen den Uhrzeigersinn können wir in ein Wandern im Uhrzeigersinn umwandeln. Man sagt, anstatt eine gewisse Zahl an Schritten gegen den Uhrzeigersinn zu wandern, muss man die Gegenzahl an Schritten im Uhrzeigersinn wandern. D.h., anstatt eine Zahl zu subtrahieren muss man ihre Gegenzahl addieren.
Im allerersten Beispiel haben wir gesehen, dass man statt 9 zu subtrahieren auch 7 addieren kann. Also ist in diesem Kreis 7 die Gegenzahl von 9.
Wenn man – so wie der Computer – alle Zahlen als Dualzahlen gegeben hat, dann kann man die Gegenzahl mit dem folgenden Verfahren bestimmen:
| Bestimmen der Gegenzahl: Invertiere in der Dualzahl alle Ziffern, d.h., aus 1 mache 0 und umgekehrt. Anschließend addiere 1 darauf. Sollte das Ergebnis mehr Stellen haben, als im Computer verwendet werden, so streiche die vorderste Stelle einfach weg. |
Schauen wir uns ein Beispiel an. Wir wollen die Gegenzahl von 0111(2) bilden. Nun sollen wir zuerst diese Zahl invertieren. Das ergibt 1000(2). Dann sollen wir 1(2) addieren. Das liefert 1001(2). Das hat nur vier Stellen, also müssen wir keine Stelle streichen. Das bedeutet statt 0111(2) zu subtrahieren können wir einfach 1001(2) addieren. Zum Beispiel:
1000(2) – 0111(2) = 1000(2) + 1001(2) = (1)0001(2)
Vorsicht! Hier müssen wir beim Endergebnis die vorderste Stelle streichen, da unser Rechenkreis nur mit vier Stellen arbeitet. Das Ergebnis lautet also 0001(2) und nicht 10001(2).
Wiedergabe stellt eine Verbindung zu YouTube her.
Zusatzwissen: Subtraktion im Dezimalsystem mit Gegenzahl
Wiedergabe stellt eine Verbindung zu YouTube her.