Mehrstufige Zufallsexperimente

Baumdiagramme und Pfadregeln

Mehrstufige Zufallsexperimente sind eine wichtige Form von Zufallsversuch. Beispiele sind das mehrfache Werfen eines Würfels, das zufällige Auswählen von mehreren Personen aus einer Gruppe nacheinander oder auch das Ziehen der Lottozahlen.

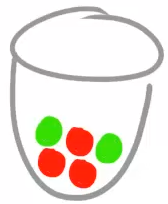
Das wichtigste Werkzeug zur Untersuchung dieser mehrstufigen Zufallsexperimente sind Baumdiagramme. Zur Einführung dieser Diagramme betrachten wir eine Urne mit zwei grünen und drei roten Kugeln. Aus dieser Urne werden nacheinander zufällig zwei Kugeln gezogen. Die erste Kugel wird nach dem Ziehen nicht zurück gelegt.

Zunächst überlegen wir, mit welchen Wahrscheinlichkeiten beim ersten Ziehen eine grüne oder rote Kugel gezogen wird.
Wir können dabei davon ausgehen, dass alle Kugeln dieselbe Wahrscheinlichkeit haben, d.h., dass ein Laplace-Versuch vorliegt. Da es insgesamt Kugeln gibt und davon grün und rot sind, haben wir diese Wahrscheinlichkeiten:

   

Diese Wahrscheinlichkeiten stellen wir etwas übersichtlicher in dieser Form dar:

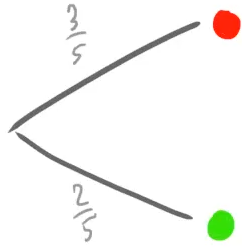
Damit machen wir deutlich, dass zwei verschiedene Möglichkeiten auftreten können und dass der Zufallsversuch dann in verschiedenen Wegen weiter ablaufen kann.

Stellen wir uns vor, wir hätten den oberen Pfad eingeschlagen, d.h., wir hätten eine rote Kugel gezogen. Dann liegen in unserer Urne noch grüne und rote Kugel. Ziehen wir jetzt noch eine zweite Kugel, dann ist die Wahrscheinlichkeit für beide Farben also jeweils .

Stellen wir uns hingegen vor, die erste Kugel wäre grün, so hätten wir nach dem ersten Ziehen nur noch eine grüne Kugel aber dafür dann rote Kugeln. In diesem Fall wäre die Wahrscheinlichkeit für Grün also nur und die für Rot läge bei .

Diese beiden unterschiedlichen Entwicklungen können wir mit einem Baumdiagramm wie in der folgenden Abbildung darstellen:

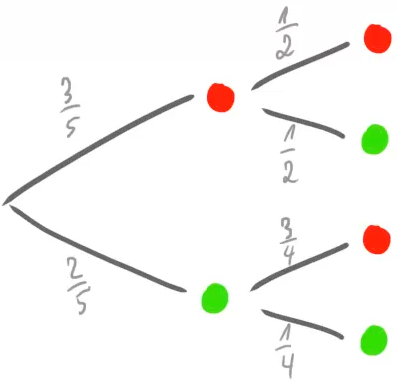
Wir können in diesem Baumdiagramm nun auf insgesamt vier verschiedenen Pfaden von ganz links nach ganz rechts wandern. Jeder Pfad stellt einen möglichen Verlauf unseres Zufallsversuchs dar. Nun stellt sich die Frage, welche Wahrscheinlichkeiten die verschiedenen Pfade haben.

Sehen wir uns z.B. den Pfad ganz oben, in dem wir zwei rote Kugeln ziehen – oder kurz – an. Führen wir den Versuch sehr häufig durch, dann werden wir in etwa der Fälle beim ersten Mal Rot ziehen. In der Hälfte dieser Fälle werden wir dann auch beim zweiten Mal Rot ziehen. Die Hälfte von ist , oder anders ausgedrückt:

   

Zum besseren Verständnis können wir uns vorstellen, dass wir den Versuch mal durchführen. In etwa der Versuche, d.h., etwa mal werden wir beim ersten Mal Rot ziehen. In etwa der Hälfte dieser Fälle, also etwa mal, werden wir dann auch beim zweiten Mal Rot ziehen. Insgesamt also in von Versuchen.
Diese Überlegung bringt uns zur Pfadmultiplikationsregel:

Pfadmultiplikationsregel: Die Wahrscheinlichkeit für einen Pfad in einem Baumdiagramm erhält man, indem man von links nach rechts den Pfad entlang wandert und die Wahrscheinlichkeiten der einzelnen Abschnitte auf dem Pfad miteinander multipliziert.

Mit dieser Regel können wir die Wahrscheinlichkeiten in unserem Baumdiagramm ergänzen:

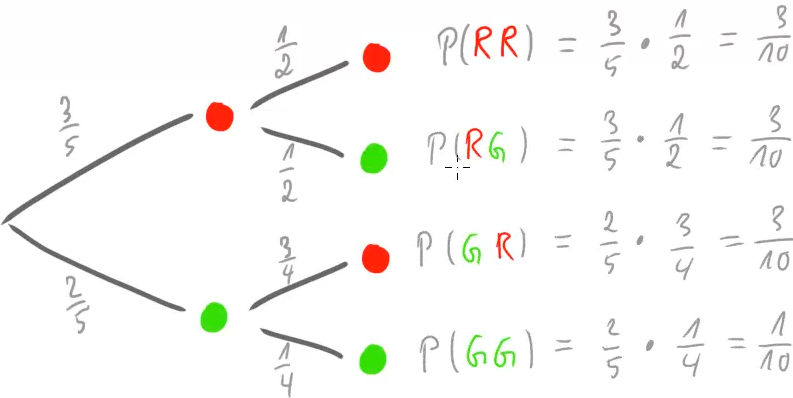
Oft interessieren uns aber nicht nur die einzelnen Pfade, sondern auch Kombinationen von ihnen. Z.B. könnten wir uns fragen, wie groß die Wahrscheinlichkeit ist, dass wir zwei verschiedene Farben ziehen. Dieses Ereignis kann auf zwei Pfaden eintreten: und . Jeder dieser Pfade hat eine Wahrscheinlichkeit von , so dass insgesamt mit einer Wahrscheinlichkeit von das Ereignis „zwei verschiedene Farben“ eintritt.
Das ist ein Beispiel zur Anwendung der Pfadadditionsregel.

Pfadadditionsregel: Gehören mehrere Pfade zu einem Ereignis, dann können wir die Wahrscheinlichkeit für das Ereignis berechnen, indem wir die Wahrscheinlichkeiten der zugehörigen Pfade addieren.

Wie groß ist also die Wahrscheinlichkeit für zwei gleichfarbige Kugeln? Das ist nun leicht für uns:

   

Anwendung und Übung zu den Pfadregeln

Wir kommen nun zu einer Übungsaufgabe. Die Lösung gibt es Clip weiter unten.

Stellen wir uns vor, wir haben in einer Schule eine Stufe mit insgesamt Schülern. In dieser Stufe gibt es einen Mathe-LK und zwei GKs:

Kurs	Anzahl Schüler
LK	24
GK1	25
GK2	26

Es werden zufällig zwei Schüler aus dieser Stufe ausgewählt. Wie groß sind dann die Wahrscheinlichkeiten für die folgenden Ereignisse?

• Es werden zwei GKler ausgewählt.
• Es werden zwei Schüler aus demselben Mathekurs ausgewählt.
• Es werden zwei Schüler aus verschiedenen Mathe-GKs ausgewählt.

Die Lösung folgt im Clip. Sie beginnt bei 1:22.

Urnenmodelle – Ziehen mit oder ohne Zurücklegen

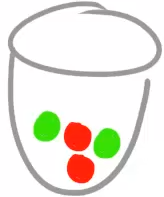
In unserer Einführung oben und auch in der Übungsaufgabe lag das Modell „Ziehen ohne Zurücklegen“ zugrunde. D.h., die Kugel bzw. der Schüler wurde nach dem ersten Ziehen nicht wieder zurück in die Urne gelegt. Dadurch mussten wir beim bestimmen der Wahrscheinlichkeiten für das zweite Ziehen immer sehr aufmerksam sein.

In manchem Anwendungen ist es aber so, dass nach dem ersten Ziehen doch wieder zurück gelegt wird. Dann können wir in jeder Stufe einfach immer wieder dieselben Wahrscheinlichkeiten an die Abzweigungen schreiben.

Das sehen wir, wenn wir unsere Urne aus der Einführung nochmal betrachten:

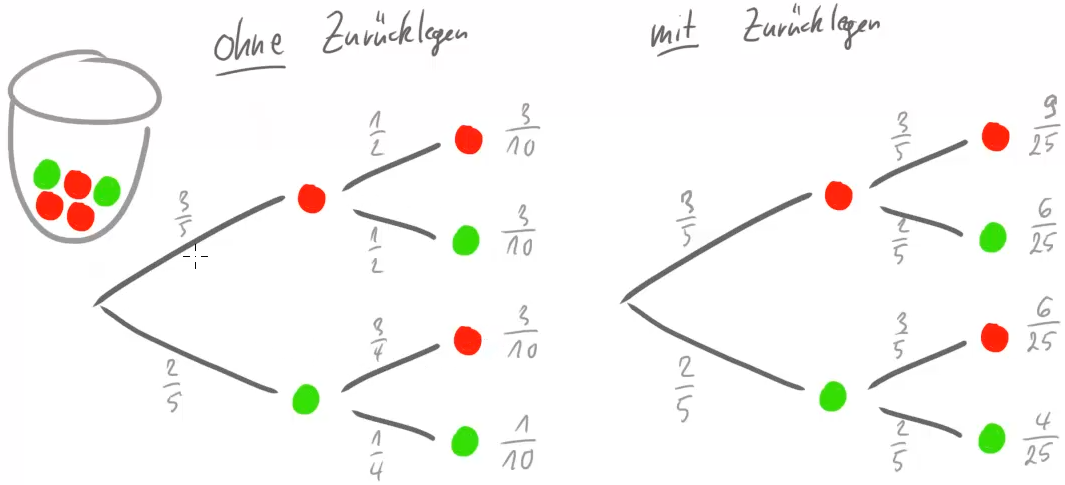
Wir müssen also bei allen Aufgaben oder Anwendungen darauf achten, ob ein Ziehen mit oder ohne Zurücklegen vorliegt. Die Wahrscheinlichkeiten können dann nämlich anders sein.

In beiden Varianten wird übrigens die Reihenfolge beachtet. Das ist wichtig, bei Formulierungen wie „Bestimme die Wahrscheinlichkeit dafür, dass einen rote und eine grüne Kugel gezogen wird“. Dafür gibt es nämlich zwei Möglichkeiten; erst Rot, dann Grün und umgekehrt. Die Wahrscheinlichkeiten von diesen zwei Möglichkeiten müssen wir addieren.