Wiedergabe stellt eine Verbindung zu YouTube her.
Daten in Tabellen
Einführung
Ausgangsituation
Nachdem wir einige erste Datenbanken konzeptioniert haben, schauen wir uns nun an, wie man aufgrund eines Konzeptes eine (erste Version einer) Datenbank realisieren kann. Wie man vielleicht schon erwartet, werden die Daten in einer Datenbank in Form von Tabellen festgehalten. Die Frage ist aber, wie man diese Tabellen geschickt gestaltet. Betrachten wir dazu das folgende Beispiel:
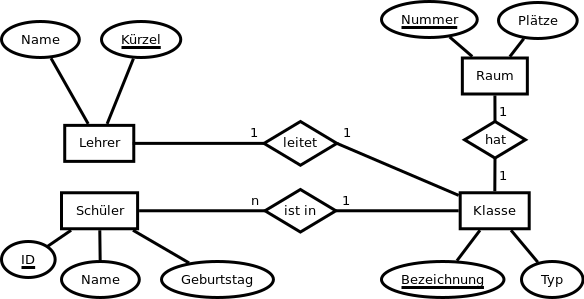
Wir schauen uns nun zwei Vorschläge dazu an, wie man die Daten in dieser Situation tabellarisch festhalten kann. Die Vorschläge sind absichtlich nicht besonders gut, um zum kritischen Mitdenken anzuregen 😉
Schlechte Umsetzung und Anomalien
Der erste Vorschlag sieht so aus:
Sekundarstufe I
| ID | Name | Geburtstag | Bez. | Raum | Plätze | Name | Kürzel | Typ |
| 54 | Spanky | 11.02.98 | 6b | 0.21 | 32 | Schmidt | Sd | bili |
| 29 | Alfalfa | 03.12.98 | 5c | 0.11 | 34 | Wessel | Wl | mont |
| 66 | Butch | 02.01.98 | 6b | 0.21 | 32 | Schmidt | Sd | bili |
| 23 | Darla | 07.06.99 | 5b | 0.10 | 34 | Weiland | Wd | reg |
| 49 | Farina | 06.04.98 | 6a | 0.22 | 30 | Gruber | Gb | mont |
| 67 | Joey | 13.01.98 | 6b | 0.21 | 32 | Schmidt | Sd | bili |
| … | … | … | … | … | … | … | … | … |
Mit dem Namen und dem Kürzel wird der Klassenlehrer angegeben.
Wir sehen schnell ein, dass dies keine praktikable Verwaltung der Daten ist.
Wenn z.B. der Klassenlehrer der 6b wechselt müssen wir bei allen Schülern dieser Klasse den Namen und das Kürzel des Lehrers aktualisieren. Das ist viel Arbeit und birgt die Gefahr, dass ein Eintrag übersehen wird. Dadurch hätten wir widersprüchliche Angaben in der Tabelle, was natürlich auf keinen Fall passieren darf. In diesem Fall sagt man, es liegt eine Dateninkonsistenz vor.
Das Übersehen eines Eintrags bei einer Änderung nennt man auch Änderungs-Anomalie.
Neben dieser gibt es auch noch die sogenannten Lösch- und Einfüge-Anomalien.
bei der Lösch-Anomalie gehen durch (gewolltes) Löschen einiger Daten auch Daten verloren, die gar nicht gelöscht werden sollen. Angenommen, der Lehrer Schmidt verlässt die Schule. Würden wir blauäugig einfach alle Zeilen mit ihm löschen, wären auch viele Schüler verschwunden!
Bei der Einfüge-Anomalie treten leere Einträge auf, obwohl man diese vielleicht gar nicht will. Hätten wir z.B. einen neuen Lehrer an der Schule, der noch keine Klasse leitet, würden wir seinen Namen und sein Kürzel ergänzen, aber der Rest der Zeile wäre leer.
Diese drei Anomalien fasst man unter dem Begriff Update-Anomalien zusammen.
Ihre Ursache liegt in der extremen Redundanz in unserer Tabelle. Das bedeutet, dass viele Informationen mehrfach in der Tabelle enthalten sind. Beispielweise die Tatsache, dass Schmidt die 6d leitet, steht bei jedem Schüler der 6d! Das ist ineffizient und führt wie oben beschrieben zu Problemen.
Wir könnten also nun auf die Idee kommen, mehr als nur eine Tabelle zu verwenden. Allerdings sollten wir dabei genau überlegen, wie wir die Tabellen aufteilen. Eine ungeschickte Aufteilung führt vielleicht zu dem folgenden Vorschlag, der auch nicht wesentlich besser ist als der erste:
Schüler
| ID | Name | Geburtstag | Raum | Name | Kürzel | Typ |
| 54 | Spanky | 11.02.1998 | 0.21 | Schmidt | Sd | bili |
| 29 | Alfalfa | 03.12.1998 | 0.11 | Wessel | Wl | mont |
| 66 | Butch | 02.01.1998 | 0.21 | Schmidt | Sd | bili |
| 23 | Darla | 07.06.1999 | 0.10 | Weiland | Wd | reg |
| 49 | Farina | 09.04.1998 | 0.22 | Gruber | Gb | mont |
| 67 | Joey | 13.01.1998 | 0.21 | Schmidt | Sd | bili |
| … | … | … | … | … | … | … |
Lehrer
| Kürzel | Bez. |
| Sd | 6b |
| Wl | 5c |
| Wd | 5b |
| Gb | 6a |
| … | … |
Raum
| Nummer | Plätze |
| 0.10 | 34 |
| 0.11 | 34 |
| 0.21 | 32 |
| 0.22 | 30 |
| … | … |
Zur Übung könntest Du die beiden Vorschläge vergleichen und überlegen, welche Schwachstellen der zweite hat.
Wiedergabe stellt eine Verbindung zu YouTube her.
Primärschlüssel
Auch in einer Tabelle hebt man durch Unterstreichung gewisse Attribute hervor. In diesem Fall unterstreicht man eine Auswahl an Attributen anhand derer man eine Zeile – oder auch Datensatz – eindeutig identifizieren kann.
Zum Beispiel kann man jede Zeile in der Tabelle Raum eindeutig am Eintrag in der Spalte Nummer identifizieren. D.h. es kann keine zwei Zeilen geben, die in der Spalte Raum denselben Eintrag haben. Oder alternativ formuliert: Es kann keine zwei Datensätze geben, in denen dass Attribut Raum denselben Wert hat.
In entsprechender Anwendungssoftware (z.B. LibreOffice Base, MS Access, DB Browser for SQLite,…) ist es auch tatsächlich nicht möglich, zwei Zeilen einzufügen, die in diesen besonderen Spalten dieselben Einträge haben.
Daher können wir die Überschrift dieser Spalte unterstreichen:
Raum
| Nummer | Plätze |
| … | … |
Man sagt nun, dass Nummer der Primärschlüssel der Tabelle Raum ist.
Auch bei Tabellen kann man oft mehrere Schlüsselkandidaten, also mögliche Kombinationen von Spalten, die einen Primärschlüssel bilden, finden.
Der Primärschlüssel hängt eng mit dem Identifikationsschlüssel aus den E-R-Diagrammen zusammen, weil die Tabellen auf Grundlage eines solchen Diagramms entstehen.
In unserem Beispiel stimmt zum der Primärschlüssel der Tabelle Raum mit dem Identifikationsschlüssel des Entitätstypen Raum überein. In der Tabelle Sekundarstufe I taucht aber zum Beispiel auch das Schlüsselattribut Bezeichnung des Klasse auf und ist in dieser Tabelle nicht notwendigerweise Teil des Primärschlüssels.
Angabe eines Datenbankschemas und Sekundärschlüssel
Betrachten wir eine weitere mögliche Umsetzung des Konzeptes zur Verwaltung der SekundarstufeI in ein Datenbankmodell:
Schüler
| ID | Name | Geburtstag | Bezeichnung |
| … | … | … | … |
Klasse
| Bezeichnung | Typ | Nummer | Kürzel |
| … | … | … | … |
Raum
| Nummer | Plätze |
| … | … |
Lehrer
| Name | Kürzel |
| … | … |
leitet
| Kürzel | Bezeichnung |
| … | … |
Wenn es so wie hier nur darum geht, die Gestalt der Tabellen zu beschreiben, aber noch keine Daten angeben will, ist es üblich, die folgende Kurzschreibweise zu verwenden:
Schüler(ID, Name, Geburtstag, ↑Bezeichnung)
Klasse(Bezeichnung, Typ, ↑Nummer, ↑Kürzel)
Raum(Nummer, Plätze, Größe)
Lehrer(Name, Kürzel)
leitet(↑Kürzel, ↑Bezeichnung)
Man sagt auch, dass diese Angaben das (relationale) Datenbankschema darstellen.
Wie bereits bei der Darstellung mittels Tabellen, werden auch hier die Primärschlüssel durch Unterstreichung kenntlich gemacht. Daneben werden aber auch einige Attribute durch einen Pfeil nach oben hervorgehoben. Mit diesem Pfeil macht man deutlich, dass es sich dabei um ein Schlüsselattribut einer anderen Tabelle handelt. Diese Attribute nennt man dann Fremdschlüssel oder auch Sekundärschlüssel.
Zum Beispiel setzt sich die Beziehung leitet zusammen aus den beiden Fremdschlüsseln Kürzel und Bezeichnung, wobei der erste auch den Primärschlüssel dieser Beziehung bildet.
Umsetzungen der Beziehungen
Wir wollen uns nun noch einmal systematisch Möglichkeiten zur Umsetzung von Beziehungen in einer Datenbank ansehen.
n:1-Beziehung
Hier haben wir als Beispiel die Beziehung ist in zwischen Schüler und Klasse.
Der gebräuchliche Weg, diese Beziehung in einem Datenbankschema umsetzen, besteht darin, in der Tabelle auf der Seite mit dem n (hier Schüler) den Primärschlüssel der anderen Tabelle (hier Bezeichnung) als Fremdschlüssel hinzuzufügen: Schüler(ID, Name, Geburtstag, ↑Bezeichnung)
Es kann passieren, dass dadurch leere Einträge entstehen. Falls es beispielsweise einen neuen Schüler gibt, der schon der Datenbank hinzugefügt werden soll, obwohl noch nicht entschieden ist, in welche Klasse er gehen wird, bleibt bei diesem die letzte Spalte leer.
1:1-Beziehung
Hier haben wir als Beispiel die Beziehung leitet zwischen Lehrer und Klasse.
Bei einer solchen Beziehung können wir wie bei einer n:1-Beziehung vorgehen. Allerdings können wir uns hier aussuchen, in welcher Tabelle wir den Fremdschlüssel der anderen ergänzen.
In unserem Beispiel scheint Klasse(Bezeichnung, Typ, ↑Nummer, ↑Kürzel) die natürlichere Wahl zu sein. Vor allem da wir mit dieser Ergänzung Lehrer(Name, Kürzel, ↑Bezeichnung) viele leere Einträge produzieren würden – bei den Lehrern, die gerade keine Klasse leitet würde nichts stehen.
An dem Schema alleine ist nun nicht mehr erkannbar, dass hier eine 1:1-Beziehung und keine n:1-Beziehung vorliegt. Daher sollte man das Diagramm immer neben dem Schema zur Hand haben, um die Übersicht zu behalten.
In der Praxis werden wir beim Erstellen der Datenbank übrigens an einer Stelle ein Häkchen setzen, um klar zu machen, dass sich das Kürzel in der Tabelle Klasse nicht wiederholen darf. Da wird also dann wieder klar sein, dass es eine 1:1-Beziehung ist.
n:m-Beziehung
Hier könnten wir in unserem Modell die Beziehung unterrichtet zwischen Lehrer und Klasse ergänzen.
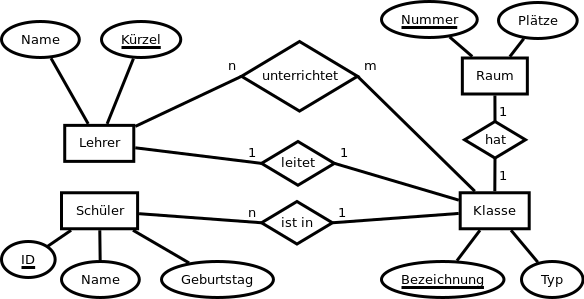
Bei einer solchen Beziehung sind wir gezwungen, eine weitere Tabelle anzulegen. In dieser stehen die Primärschlüssel der beiden beteiligten Tabellen als Fremdschlüssel. Sie bilden zusammen den Primärschlüssel der neuen Tabelle: unterrichtet(↑Bezeichnung, ↑Kürzel)
Es müssen wirkliche beide Fremdschlüssel unterstrichen werden! Wäre z.B. nur Kürzel unterstrichen, könnte jeder Lehrer nur einmal aufgeführt werden und somit nur eine Klasse unterrichten.
Beispiel
Wenn wir die Modellierung der Sekundarstufe I aus dem Diagramm also nun umsetzen, kommen wir zum Beispiel zu diesem Ergebnis:
Schüler(ID, Name, Geburtstag, ↑Bezeichnung)
Klasse(Bezeichnung, Typ, ↑Nummer, ↑Kürzel)
Raum(Nummer, Plätze, Größe)
Lehrer(Name, Kürzel)
unterrichtet(↑Bezeichnung, ↑Kürzel)