2.08 Abstrakte Klassen & Interfaces

Abstrakte Klassen

Wenn wir über abstrakte Klassen reden, bedeutet dies nicht etwa, dass wir über besonders komplizierte Klassen sprechen. Das will ich betonen, da in der Alltagssprache das Wort „abstrakt“ oft im Sinne von „kompliziert“ verwendet wird. Wir sollten „abstrakt“ eher als „sehr allgemein“ verstehen oder auch als Gegenteil von „konkret“. Mit einem Beispiel wird dies deutlich.

Nehmen wir an, wir wollen ein kleines Tool für geometrische Berechnungen entwerfen. Dabei wollen wir verschiedene geometrische Formen untersuchen, zum Beispiel Rechtecke und Kreise. Uns scheint es sinnvoll, entsprechende Klassen Rechteck und Kreis zu verwenden und diese von einer gemeinsamen Oberklasse abzuleiten. Nun stellt sich die Frage, welche gemeinsame Oberklasse in Frage kommt.

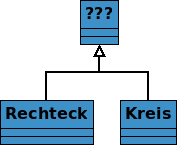
Überlegen wir dazu einmal, welche Gemeinsamkeiten die beiden Unterklassen haben sollen. Es wäre schließlich sinnvoll, diese Gemeinsamkeiten dann mithilfe der Oberklasse umzusetzen. Wir begnügen uns für den Moment mit diesen beiden Punkten:

• Wir möchten gerne mit Koordinaten angeben, wo sich ein Objekt befindet.
• Wir möchten eine Methode zur Berechnung des Flächeninhalts haben.

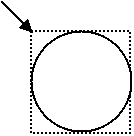
Mit den Koordinaten ist damit – wie in Java üblich – die linke obere Ecke gemeint. Bei einem Kreis müssen wir uns vorstellen, dass sich dieser in einem Quadrat befindet. Dann ist von diesem Quadrat die linke obere Ecke gemeint.

---

Hintergrundinformation

Die etwas ungewohnte Festlegung der Koordinaten – vor allem beim Kreis – orientiert sich an den Zeichenmethoden in Java. Diese werden wir uns auch noch ansehen. Damit wir dann nicht wieder umdenken müssen, führen wir hier schon diese Art der Angabe der Koordinaten ein.
Es geht sogar noch weiter. Bei der Angabe der Koordinaten im Bildschirm befindet sich der Ursprung in der Ecke oben links. D.h., die x-Achse verläuft wie gewohnt von links nach rechts, die y-Achse aber von oben nach unten. Das ist für unsere Beispiele in dieser Lektion aber nicht wichtig.

---

Halten wir zunächst diese beiden Ideen fest. Als Name für die Oberklasse können wir Figur verwenden, da dieser recht allgemein ist:

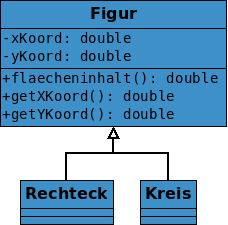
Nun stehen wir allerdings vor einem Problem. Wie soll die Methode flacheninhalt() der Oberklasse aussehen? Schließlich werden der Flächeninhalt eines Rechtecks und eines Kreises doch vollkommen verschieden berechnet.

Die Lösung ist, dass wir in der Oberklasse diese Methode als sogenannte abstrakte Methode kennzeichnen! Das bedeutet, dass wir zwar festlegen, dass diese Methode vorhanden sein soll, aber gleichzeitig in der Oberklasse noch gar nichts über deren Funktionsweise angeben. Schauen wir uns dies einmal an:

public abstract class Figur {
  
  // Attribute
  protected double xKoord;
  protected double yKoord;
  
  // Konstruktor
  public Figur(double pXKoord, double pYKoord){
    xKoord = pXKoord;
    yKoord = pYKoord;
  }
  
  // abstrakte Methode
  abstract double flaecheninhalt();
  
  // Ausgabe
  public String toString(){
    return "("+xKoord+"|"+yKoord+")";
  }

  // get-Methoden
  public double getxKoord() {
    return xKoord;
  }

  public double getyKoord() {
    return yKoord;
  }

}

Die Methode flaecheninhalt() wurde hier also mit dem Schlüsselwort abstract versehen. Es wurde auch angegeben, dass sie einen double-Wert zurückgeben soll. Anstatt einer Implementierung der Methode finden wir danach aber nur ein Semikolon.

Übrigens wurde auch die Klasse selbst als abstrakt gekennzeichnet, wie wir in der ersten Zeile sehen. Das müssen wir so implementieren, denn sobald eine Klasse eine abstrakte Methode besitzt, ist automatisch die gesamte Klasse abstrakt.

Wir haben in dieser Klasse auch noch eine toString()-Methode, die lediglich die Koordinaten angibt und daneben noch die üblichen get-Methoden.

Diese Klasse können wir noch nicht testen. Wenn wir versuchen ein Objekt dieser Klasse zu erstellen, erhalten wir eine Fehlermeldung:

public class Figurtest {

  public static void main(String[] args) {
    
    Figur meineFigur = new Figur(100, 100);
    // Fehler: Cannot instantiate the type Figur

  }

}

Nun kann man sich natürlich fragen, wozu diese Klasse gut sein soll, wenn man sie nicht verwenden kann!?

Der Punkt ist, dass diese Klasse dazu da ist, einen Rahmen dafür vorzugeben, wie die Unterklassen Rechteck und Kreis auszusehen haben. Vor allem wird nun verlangt, dass diese beiden Klassen die Methode flaecheninhalt() besitzen!

Die Klasse Rechteck können wir nun so implementieren:

public class Rechteck extends Figur {

  private double breite;
  private double hoehe;

  public Rechteck(double pXKoord, double pYKoord, double pBreite, double pHoehe){
    super(pXKoord, pYKoord);
    breite = pBreite;
    hoehe = pHoehe;
  }

  public double flaecheninhalt() {
    return breite*hoehe;
  }

  public String toString(){
    return "Rechteck mit Eckpunkt "+super.toString()+", Breite "+breite+" und "+hoehe;
  }

}

Der Flächeninhalt wird beim Rechteck natürlich einfach berechnet, indem man die Breite und die Höhe multipliziert. Dass die Oberklasse Figur tatsächlich einen Zweck erfüllt, erkennen wir, wenn wir in Rechteck die Methode flaecheninhalt() einmal entfernen oder auskommentieren. Es erscheint prompt eine Fehlermeldung, da die abstrakte Klasse Figur verlangt, dass flaecheninhalt() implementiert wird.

Diese Klasse besitzt ebenfalls eine toString()-Methode, die auf die entsprechende Methode der Oberklasse zurückgreift.

---

TIPP

Eine solche Festlegung mithilfe einer abstrakten Klasse könnte beispielsweise in einer Projektarbeit, an der mehrere Personen beteiligt sind, nützlich sein. Vielleicht könntest Du tatsächlich in einem Team ein echtes Geometrie-Tool erstellen. Ihr könntet dann verschiedene geometrische Formen von verschiedenen Teammitgliedern erstellen lassen. Damit am Ende alles gut zusammenpasst, könnt Ihr mithilfe einer abstrakten Oberklasse bestimmte Vorgaben treffen, an die sich dann alle zu halten haben.

---

Nun sollten wir natürlich auch noch die Klasse Kreis implementieren. Der Flächeninhalt eines Kreises ist gegeben durch , wobei der Radius ist. An eine sehr genaue Annäherung von kommen wir Math.PI:

public class Kreis extends Figur {

  private double radius;
   
  public Kreis(double pXKoord, double pYKoord, double pRadius){
    super (pXKoord, pYKoord);
    radius = pRadius;
  }
  
  public double flaecheninhalt() {
    return Math.PI*radius*radius;
  }
  
  public String toString(){
    return "Kreis mit Radius "+radius;
  }

}

Wie oben bereits erklärt, sind die Koordinaten hier nicht die Koordinaten des Mittelpunktes. Das ist natürlich etwas ungewohnt. Daher wollen wir gerne auch den Mittelpunkt ergänzen.

Außerdem möchten wir noch eine weitere Methode enthaelt ergänzen. Mit dieser soll man prüfen können, ob ein gegebener Punkt in einer Figur enthalten ist oder außerhalb der Figur liegt. Zur Übung bietet es sich bei dieser Gelegenheit auch noch an, eine weitere Klasse Punkt einzuführen und damit die Assoziation zu wiederholen.

Sehen wir uns zuerst unser Vorhaben in einem Diagramm an:

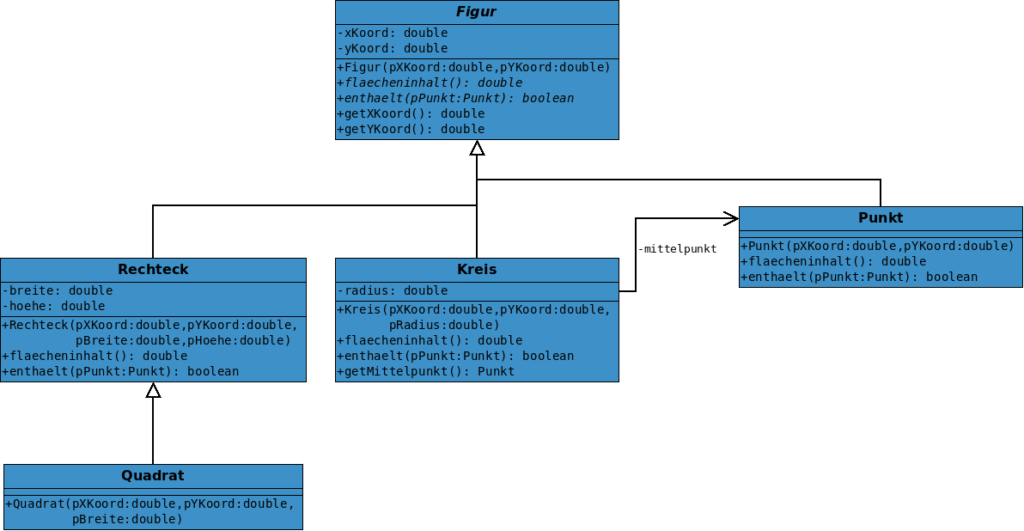
Da dies das erste Klassendiagramm in dieser Lektion ist, in dem wir genau angeben, was wir implementieren, sollten wir hier auch gründlich die abstrakten Klassen und Methoden hervorheben. Ein üblicher Weg dafür besteht darin, sie kursiv zu schreiben. Wird eine Methode dann in einer Unterklasse implementiert, wird sie dort nochmal aufgeführt aber dann natürlich nicht mehr kursiv.

Sehen wir uns noch die weiteren Punkte an, die hier geplant wurden:

• Die abstrakte Klasse Figur hat die zusätzliche abstrakte Methode enthaelt erhalten. Diese verlangt als Parameter ein Objekt der Klasse Punkt und liefert einen Wahrheitswert als Ergebnis. Dadurch muss diese Methode auch in den anderen Klassen implementiert werden!
• Diese Klasse Punkt wurde ergänzt. Auch sie ist Unterklasse von Figur.
• Ein Kreis hat ab nun einen Mittelpunkt. Dieser Mittelpunkt ist ein Objekt der Klasse Punkt.
• Die Klasse Rechteck erhält zur Übung noch eine Unterklasse Quadrat, denn Quadrate sind ja spezielle Rechtecke.

Sehen wir uns zunächst die neue Version von Figur an:

public abstract class Figur {
  
  // Attribute
  protected double xKoord;
  protected double yKoord;
  
  // Konstruktor
  public Figur(double pXKoord, double pYKoord){
    xKoord = pXKoord;
    yKoord = pYKoord;
  }
  
  // abstrakte Methode
  abstract double flaecheninhalt();
  
  abstract boolean enthaelt(Punkt pPunkt);
  
  // Ausgabe
  public String toString(){
    return "("+xKoord+"|"+yKoord+")";
  }

  // get-Methoden
  public double getxKoord() {
    return xKoord;
  }

  public double getyKoord() {
    return yKoord;
  }

}

Im Vergleich zu vorher wurde lediglich die abstrakte Methode enthaelt ergänzt. Entsprechend haben wir in Rechteck nun eine Implementierung dieser Methode:

public class Rechteck extends Figur {

    private double breite;
    private double hoehe;

    public Rechteck(double pXKoord, double pYKoord, double pBreite, double pHoehe){
        super(pXKoord, pYKoord);
        breite = pBreite;
        hoehe = pHoehe;
    }

    public double flaecheninhalt() {
        return breite*hoehe;
    }

    public boolean enthaelt(Punkt pPunkt){
        return (pPunkt.getxKoord() >= xKoord && pPunkt.getxKoord() <= breite+xKoord && 
                pPunkt.getyKoord() >= yKoord && pPunkt.getyKoord() <= hoehe+yKoord);        
    }

    public String toString(){
        return "Rechteck mit Eckpunkt "+super.toString()+", Breite "+breite+" und "+hoehe;
    }

}

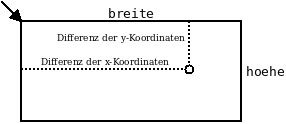
Diese Methode vergleicht die Koordinaten des Objekts pPunkt mit denen des Rechtecks. Die x-Koordinate des Punktes muss zwischen der x-Koordinate der linken oberen Ecke des Rechtecks – also xKoord – und xKoord+breite liegen, damit der Punkt im Rechteck liegt. Entsprechendes gilt für die y-Koordinate. Das Bild soll dies noch ein wenig veranschaulichen.

Sehen wir uns nun die neue Version der Klasse Kreis an:

public class Kreis extends Figur {

    private double radius;
    private Punkt mittelpunkt;
    
    public Kreis(double pXKoord, double pYKoord, double pRadius){
        super (pXKoord, pYKoord);
        radius = pRadius;
        mittelpunkt = new Punkt(pXKoord+radius, pYKoord+radius);
    }
    
    public double flaecheninhalt() {
        return Math.PI*radius*radius;
    }
    
    public boolean enthaelt(Punkt pPunkt){
        return (Math.sqrt( (pPunkt.getxKoord()-xKoord)*(pPunkt.getxKoord()-xKoord)+(pPunkt.getyKoord()-yKoord)*(pPunkt.getyKoord()-yKoord) )<= radius);
    }
        
    public String toString(){
        return "Kreis mit Mittelpunkt "+mittelpunkt+" und Radius "+radius;
    }
    
    public Punkt getMittelPunkt(){
        return mittelpunkt;
    }

}

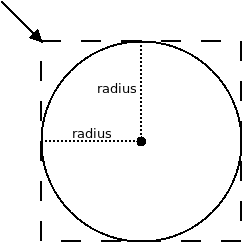
Wir sehen, dass das neue Attribut mittelpunkt hinzugefügt wurde. Wo dieser Mittelpunkt liegt, wird im Konstruktor automatisch ermittelt – er muss also nicht als Parameter übergeben werden. Wie die Berechnung funktioniert, wird in der Abbildung angedeutet.

Die Methode enthaelt sieht hier natürlich anders aus als bei der Klasse Rechteck. Hier nutzen wir aus, dass ein Punkt genau dann im Kreis liegt, wenn sein Abstand zum Mittelpunkt kleiner oder gleich dem Radius ist. Mit anderen Worten, ein Punkt liegt im Kreis mit Mittelpunkt und Radius genau dann, wenn

   

Falls Dir diese Formel zur Berechnung des Abstands zweier Punkte nicht bekannt ist, ist das nicht weiter schlimm. Man kann sie mit dem Satz des Pythagoras herleiten. Wichtiger ist vielleicht, dass Du nachvollziehen kannst, dass sie in der Implementierung tatsächlich verwendet wird.

Nun haben wir schon die Klasse Punkt benutzt, diese aber noch gar nicht betrachtet. Sie ist aber zum Glück deutlich einfacher als die anderen Klassen:

public class Punkt extends Figur {

  public Punkt(double pXKoord, double pYKoord){
    super(pXKoord, pYKoord);
  }
  
  double flaecheninhalt() {
    return 0;
  }

  public boolean enthaelt(Punkt pPunkt){
    return (xKoord == pPunkt.getxKoord() && yKoord == pPunkt.getyKoord());
  }
  
}

Der Flächeninhalt eines Punktes ist 0. Ein Punkt enthält einen anderen Punkt nur, wenn er dieselben Koordinaten hat.

Die Klasse Quadrat ist ebenfalls recht simpel:

public class Quadrat extends Rechteck {
  
  public Quadrat(int pXKoord, int pYKoord, int breite){
    super (pXKoord, pYKoord, breite, breite);
  }
  
}

Hier sollte uns lediglich noch einmal vor Augen geführt werden, inwiefern ein Quadrat eine Spezialisierung eines Rechtecks ist.

Kommen wir zu einem abschließenden Test unserer Klassen:

public class Figurtest {

  public static void main(String[] args) {
    
    Rechteck meinRechteck = new Rechteck(100, 100, 40, 20);
    System.out.println(meinRechteck);
    System.out.println(meinRechteck.flaecheninhalt());
    System.out.println(meinRechteck.enthaelt(new Punkt(120,110)));
    System.out.println(meinRechteck.enthaelt(new Punkt(90,110)));
    
    Kreis meinKreis = new Kreis(400, 200, 10);
    System.out.println(meinKreis);
    System.out.println(meinKreis.flaecheninhalt());
    System.out.println(meinKreis.enthaelt(new Punkt(400,210)));
    
    Quadrat meinQuadrat = new Quadrat(400, 200, 20);
    System.out.println(meinQuadrat);
    System.out.println(meinQuadrat.flaecheninhalt());
    System.out.println(meinQuadrat.enthaelt(meinKreis.getMittelPunkt()));

  }

}

Hier werden die verschiedenen Methoden getestet. In der letzten Ausgabe wird übrigens angezeigt, ob der Mittelpunkt des Kreises im Quadrat liegt. Wir erhalten folgende Ausgaben:

Rechteck mit Eckpunkt (100.0|100.0), Breite 40.0 und 20.0
800.0
true
false
Kreis mit Mittelpunkt (410.0|210.0) und Radius 10.0
314.1592653589793
true
Rechteck mit Eckpunkt (400.0|200.0), Breite 20.0 und 20.0
400.0
true

Interfaces / Schnittstellen

Es gibt in Java noch eine Steigerung von abstrakten Klassen: Die sogenannten Interfaces oder auch Schnittstellen. Grob gesprochen besteht ein Interface nur noch aus abstrakten Methoden – bei abstrakten Klassen können ja auch einige Methoden bereits implementiert sein und es kann Attribute sowie einen Konstruktor geben.

Sehen wir uns eine Änderung unseres Beispiels von oben an, bei der auch ein Interface vorkommt:

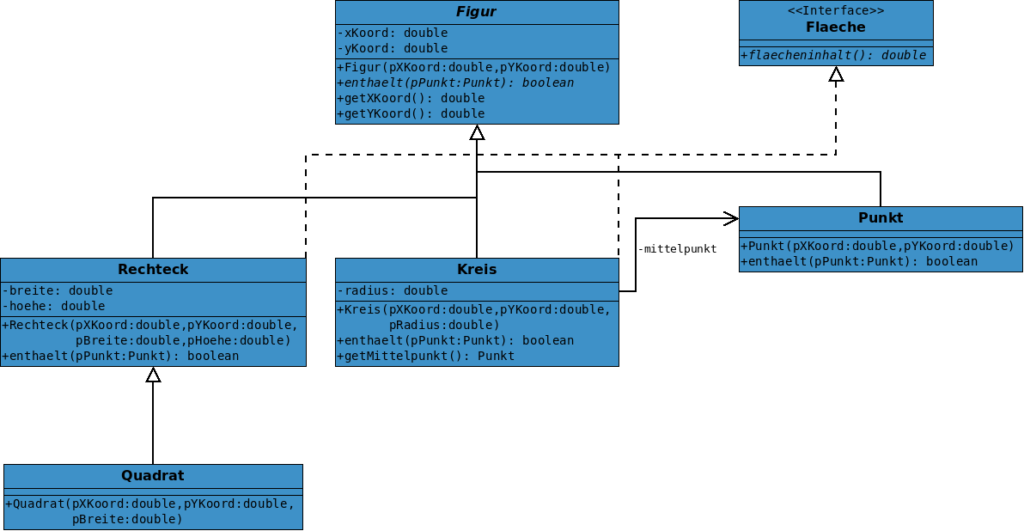
Die abstrakte Klasse Figur hat nun nicht mehr die abstrakte Methode flaecheninhalt(). Stattdessen haben wir nun das Interface Flaeche, das einzig und allein genau diese abstrakte Methode vorgibt. Die Klassen Rechteck und Kreis implementieren dieses Interface – oder wie man auch sagt, sie realisieren dieses Interface. Daher sagt uns dieses Diagramm, dass sie diese Methode besitzen müssen. Die Klasse Punkt hingegen implementiert dieses Interface nicht, da ein Punkt keinen Flächeninhalt besitzt.

Wir könnten nun noch weitere Figuren hinzufügen und jeweils überlegen, ob sie in vernünftiger Weise einen Flächeninhalt besitzen. Eine Gerade beispielsweise nicht, so dass eine entsprechende Klasse auch nicht dieses Interface implementieren würde. Eine Klasse Dreieck sollte dies hingegen doch.

Vielleicht ist Dir etwas eigenartiges aufgefallen: In dem Diagramm sieht es nun so aus, als hätten Rechteck und Kreis zwei Oberklassen, nämlich Figur und Flaeche. Dabei ist das in Java doch verboten!? In der Tat umgehen Interfaces dieses Verbot, so dass sie im Vergleich zu Klassen etwas aus dem Rahmen fallen. Böse formuliert könnte man sagen, wir haben wir nun Mehrfachvererbung über eine Hintertür erreicht.

Kommen wir nun zur Implementierung. Das Interface können wir so programmieren:

public interface Flaeche {
  
  public double flaecheninhalt();

}

Das ist nun wirklich nicht viel. Beachte hier aber, dass die Methode nicht als abstrakt deklariert werden muss. In einem Interface sind immer alle Methoden automatisch abstrakt.

Die abstrakte Klasse Figur hat, wie schon erwähnt, nicht mehr die Methode flaecheninhalt(). Ansonsten ändert sich nichts:

public abstract class Figur {
  
  // Attribute
  protected double xKoord;
  protected double yKoord;
  
  // Konstruktor
  public Figur(double pXKoord, double pYKoord){
    xKoord = pXKoord;
    yKoord = pYKoord;
  }
  
  // abstrakte Methode	
  abstract boolean enthaelt(Punkt pPunkt);
  
  // Ausgabe
  public String toString(){
    return "("+xKoord+"|"+yKoord+")";
  }

  // get-Methoden
  public double getxKoord() {
    return xKoord;
  }

  public double getyKoord() {
    return yKoord;
  }

}

Nun sehen wir, wie wir kenntlich machen, dass die Klasse Kreis das Interface implementiert:

public class Kreis extends Figur implements Flaeche{

  private double radius;
  private Punkt mittelpunkt;
  
  public Kreis(double pXKoord, double pYKoord, double pRadius){
    super (pXKoord, pYKoord);
    radius = pRadius;
    mittelpunkt = new Punkt(pXKoord+radius, pYKoord+radius);
  }
  
  public double flaecheninhalt() {
    return Math.PI*radius*radius;
  }
  
  public boolean enthaelt(Punkt pPunkt){
    return (Math.sqrt( (pPunkt.getxKoord()-xKoord)*(pPunkt.getxKoord()-xKoord)+(pPunkt.getyKoord()-yKoord)*(pPunkt.getyKoord()-yKoord) )<= radius);
  }
    
  public String toString(){
    return "Kreis mit Mittelpunkt "+mittelpunkt+" und Radius "+radius;
  }
  
  public Punkt getMittelPunkt(){
    return mittelpunkt;
  }

}

Neben der Angabe extends Figur haben wir nun zusätzlich noch die Angabe implements Flaeche. Theoretisch dürften wir an dieser Stelle übrigens sogar noch mehr Interfaces auflisten.

Die Klasse Rechteck wird in derselben Weise angepasst:

public class Rechteck extends Figur implements Flaeche{

  private double breite;
  private double hoehe;

  public Rechteck(double pXKoord, double pYKoord, double pBreite, double pHoehe){
    super(pXKoord, pYKoord);
    breite = pBreite;
    hoehe = pHoehe;
  }

  public double flaecheninhalt() {
    return breite*hoehe;
  }

  public boolean enthaelt(Punkt pPunkt){
    return (pPunkt.getxKoord() >= xKoord && pPunkt.getxKoord() <= breite+xKoord && 
        pPunkt.getyKoord() >= yKoord && pPunkt.getyKoord() <= hoehe+yKoord);		
  }

  public String toString(){
    return "Rechteck mit Eckpunkt "+super.toString()+", Breite "+breite+" und "+hoehe;
  }

}

Die Klasse Quadrat bleibt als einzige unverändert:

public class Quadrat extends Rechteck{
  
  public Quadrat(int pXKoord, int pYKoord, int breite){
    super (pXKoord, pYKoord, breite, breite);
  }
  
}

Dies ist natürlich nur eine kleine Anregung für ein Geometrie-Tool. In erster Linie ging es in dieser Lektion schließlich um das Konzept einer abstrakten Klasse. Aber vielleicht hast Du ja Lust, dieses Beispiel noch weiter auszubauen.