03 Addierer

Halbaddierer

Unser erster Schritt wird es sein, eine Schaltung zu konstruieren, mit der wir zwei einstellige Binärzahlen addieren können. Das ist natürlich ein sehr bescheidener Start, aber mithilfe dieser Konstruktion können wir dann schrittweise immer aufwändigere Schaltungen entwerfen.

Bei der Addition zweier Binärzahlen mit jeweils nur einer Stelle gibt es nur vier mögliche Fälle:

0₍₂₎ + 0₍₂₎ = 0₍₂₎
0₍₂₎ + 1₍₂₎ = 1₍₂₎
1₍₂₎ + 0₍₂₎ = 1₍₂₎
1₍₂₎ + 1₍₂₎ = 10₍₂₎

Der letzte Fall ist dabei etwas besonderes, weil es der einzige ist, bei dem ein Übertrag auftritt. Mit anderen Worten, es ist der einzige, bei dem das Ergebnis zweistellig ist.

Etwas deutlicher wird dies noch in dieser Tabelle, anhand derer wir dann überlegen, wie wir diese Addition mithilfe einer Schaltung darstellen:

1. Zahl	2. Zahl	Übertrag	Summe
0(2)	0(2)	0(2)	0(2)
0(2)	1(2)	0(2)	1(2)
1(2)	0(2)	0(2)	1(2)
1(2)	1(2)	1(2)	0(2)

Wir sehen nun recht deutlich:

• Der Übertrag ist nur dann 1₍₂₎, wenn beide Summanden 1₍₂₎ sind.
• Die Summe ist nur dann 1₍₂₎, wenn entweder der erste oder der zweite Summand 1₍₂₎ sind.

Damit erkennen wir, welche Bauteile wir benötigen. Der Übertrag zeigt nämlich genau das Verhalten eines UND-Gatters. Die Summe hingegen verhält sich genau wie ein EXOR-Gatter. Die beiden Summanden können wir natürlich am besten mit Schaltern darstellen und die Ergebnisse mit LEDs:

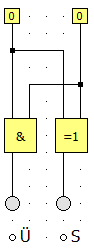
Eine Schaltung, wie wir sie nun konstruiert haben, nennt man Halbaddierer. Einen Halbaddierer stellt man in größeren Schaltungen oft in so einer kompakten Form dar:

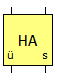
Wenn man aufwändige Schaltungen konstruiert, ist es sogar sehr zu empfehlen, einzelne Komponenten in so einer kompakten Weise darzustellen, da die Schaltungen sonst kaum noch zu durchschauen sind.

An die oberen Leitungen können wir wieder die zwei Schalter anbringen und unten die LEDs. Wir können die Ergebnisse, die wir an den unteren Leitungen erhalten aber auch anders verwenden. Zum Beispiel, um weitere Rechnungen anzustellen.

Volladdierer

Man könnte im ersten Moment glauben, dass wir damit schon eine Schaltung bauen können, mit der man mehrstellige Dualzahlen addieren kann. Zum Beispiel diese:

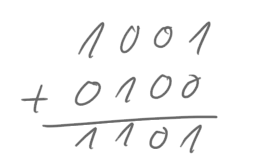
Ein Vorschlag, um eine Schaltung zu konstruieren, mit den man beispielsweise vierstellige Dualzahlen addieren kann, könnte sein, dass man einfach vier Halbaddierer nebeneinander baut. Der Halbaddierer ganz rechts addiert die Einer, der links daneben die Zweier, der nächste die Vierer und der ganz links die Achter.

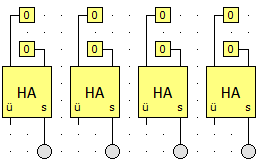
Diese Schaltung würde zwar die Addition aus dem Beispiel von oben korrekt darstellen, aber sobald ein Übertrag auftritt, liefert sie falsche Ergebnisse. Die Überträge werden hier ja überhaupt nicht berücksichtigt.

Nun stehen wir aber vor einem Problem: Die Überträge müssten eigentlich von rechts nach links immer weitergereicht werden, so wie in einer schriftlichen Addition:

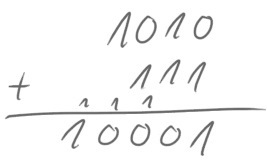
Dafür müssten aber alle Halbaddierer bis auf den ganz rechts drei Eingänge besitzen; zwei für die Zahlen die addiert werden sollen und einen für den Übertrag.

So ein Addierer mit drei Eingängen heißt nicht mehr Halbaddierer sondern Volladdierer. Es gibt verschiedene Möglichkeiten, so einen Volladierer zu konstruieren. Wir könnten wie beim Halbaddierer mit einer Tabelle genau untersuchen, wann die Summe und der Übertrag 1₍₂₎ sind und dann mit den entsprechenden Grundbausteinen eine passende Schaltung erstellen. (Als Übung ist das tatsächlich eine gute Idee!)

Wir verwenden hier aber eine einfachere Bauweise:

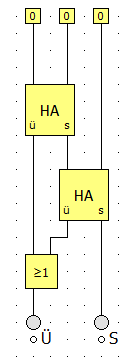
Warum liefert diese Schaltung das richtige Ergebnis? Um das einzusehen, können wir uns vorstellen, dass zuerst die beiden linken Zahlen (d.h. die, die mit den linken Schaltern dargestellt werden) addiert werden. Tritt dabei schon ein Übertrag auf, wird er unten an das ODER-Gatter geleitet. Die Summe wird im zweiten Halbaddierer mit der noch fehlenden dritten Zahl addiert. So erhalten wir schließlich die Endsumme und auch hier möglicherweise noch einen Übertrag. Ist in mindestens einem der beiden Schritte ein Übertrag entstanden, dann wird dieser unten ausgegeben.

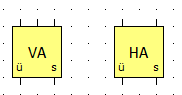
Uns stehen also nun zwei neue Bausteine zur Verfügung: Halb- und Volladdierer.

4-Bit-Addierer

Unser nächstes Ziel ist es, mit unseren neuen Bausteinen mehrstellige Zahlen zu addieren. Noch können wir ja nur einstellige Zahlen addieren.

Wir wollen uns dazu einmal anschaulich vorstellen, wie man mithilfe eines Halb- und eines Volladdierers zwei zweistellige Dualzahlen addieren kann. Dafür stellen wir uns die beiden Addierer ganz menschlich vor:

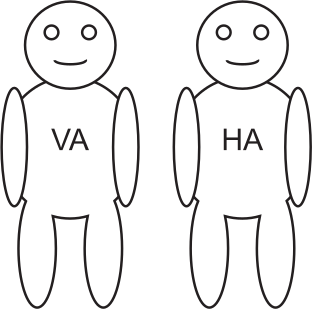
Der Halbaddierer soll für uns die Einer addieren und der Volladdierer soll den Rest erledigen, d.h., die Zweier und den möglichen Übertrag addieren. Nehmen wir als Beispiel diese Rechnung:

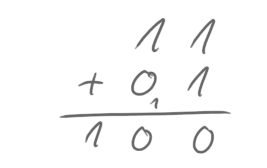
Damit die beiden die Rechnung ausführen können, müssen wir ihnen erst einmal die Zahlen mitteilen. Dazu erhält der Halbaddierer die beiden Einerstellen und der Volladdierer die beiden Zweierstellen, die sie sich jeweils merken:

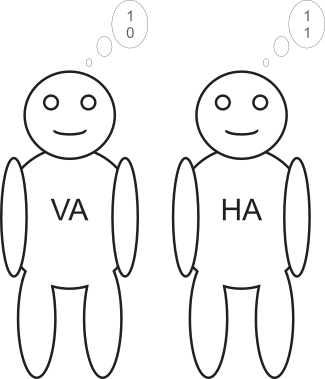
Als erster beginnt der Halbaddierer mit der Arbeit, denn man muss bei der Addition ja immer ganz rechts bei den Einern starten. Er erhält als Summe eine 0₍₂₎ – wie oben in der Rechnung – und außerdem einen Übertrag von 1₍₂₎. Diesen Übertrag hält er dem Volladdierer unter die Nase, da er diesen bei der weiteren Rechnung beachten muss:

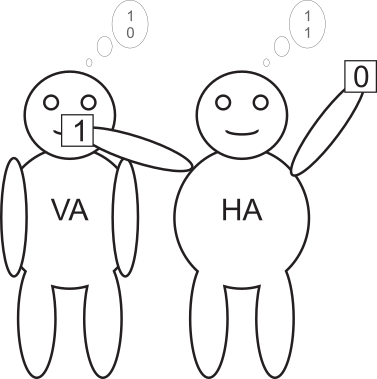
Nun muss der Volladdierer die beiden gemerkten Zahlen und den Übertrag addieren und uns das Ergebnis mitteilen:

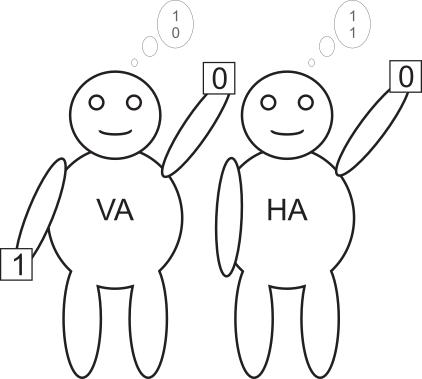
Den Rechenvorgang, den wir uns oben anschaulich mit zwei Männchen vorgestellt haben, können wir  nun in eine Schaltung übertragen:

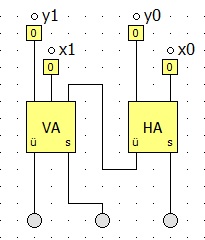
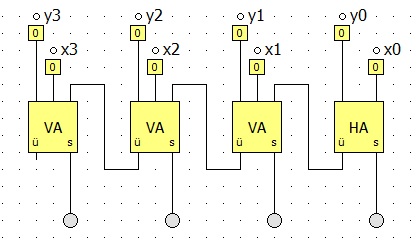
Der Knackpunkt ist hier das Weiterleiten des Übertrags in den Volladdierer. Nach diesem Muster können wir jetzt die Schaltung beliebig erweitern. So sieht zum Beispiel ein 4-Bit-Addierer aus: